矩阵(题单顺序)
热题 100 - 矩阵分组(按题单顺序):73 / 54 / 48 / 240
本页包含题单「矩阵」分组的全部题目,顺序与 list.json 保持一致。
73. 矩阵置零
给定一个 m x n 的矩阵,如果一个元素为 0 ,则将其所在行和列的所有元素都设为 0 。请使用 原地 算法。
示例 1:

输入:matrix = [[1,1,1],[1,0,1],[1,1,1]] 输出:[[1,0,1],[0,0,0],[1,0,1]]
示例 2:

输入:matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]] 输出:[[0,0,0,0],[0,4,5,0],[0,3,1,0]]
提示:
m == matrix.lengthn == matrix[0].length1 <= m, n <= 200-231 <= matrix[i][j] <= 231 - 1
进阶:
- 一个直观的解决方案是使用
O(mn)的额外空间,但这并不是一个好的解决方案。 - 一个简单的改进方案是使用
O(m + n)的额外空间,但这仍然不是最好的解决方案。 - 你能想出一个仅使用常量空间的解决方案吗?
最优解(原地标记:用第一行/第一列当“记号板”)
正在加载编辑器...
最优解讲解(通俗版 + 推理过程)
- 题意翻译:只要某个格子是 0,就要把它所在整行整列都变成 0,并且要原地做。
- 朴素做法的坑:你如果边扫边改,一旦把某个格子改成 0,会“污染”后续判断,导致清零范围无限扩大。
- 正确做法必须分两步:
- 先“记录”哪些行/列需要清零
- 再统一执行清零
- 为什么不用额外数组也能记录?:把第一行/第一列当“记号板”:
- 当发现
matrix[i][j]==0,就做标记:matrix[i][0]=0(第 i 行要清零)、matrix[0][j]=0(第 j 列要清零)。
- 当发现
- 但是第一行/第一列本身怎么办?:它们既当数据又当标记,必须单独记录:
- 用
firstRowZero / firstColZero先记住第一行/第一列是否原本就含 0。
- 用
- 执行顺序为什么重要?
- 标记阶段从 (1,1) 开始,避免直接覆盖第一行/列的“是否清零信息”。
- 清零阶段也从 (1,1) 开始,最后再看
firstRowZero/firstColZero处理第一行/列。
- 复杂度:两趟扫描,时间 (O(mn)),额外空间 (O(1))。
- 最常见坑:忘记单独处理第一行/第一列,导致标记被覆盖后信息丢失。
- 为什么要“先标记再清零”?:因为清零会改变原矩阵,如果一边扫一边清,会把新产生的 0 当成“原本就有的 0”,造成错误扩散。
类似题目(原地标记:用边界当标记位)
// 典型套路:把某一行/列/区域当做“标记数组”,再二次遍历应用标记
54. 螺旋矩阵
给你一个 m 行 n 列的矩阵 matrix ,请按照 顺时针螺旋顺序 ,返回矩阵中的所有元素。
示例 1:

输入:matrix = [[1,2,3],[4,5,6],[7,8,9]] 输出:[1,2,3,6,9,8,7,4,5]
示例 2:

输入:matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]] 输出:[1,2,3,4,8,12,11,10,9,5,6,7]
提示:
m == matrix.lengthn == matrix[i].length1 <= m, n <= 10-100 <= matrix[i][j] <= 100
最优解(四个边界:上/下/左/右,按圈走)
正在加载编辑器...
最优解讲解(通俗版 + 推理过程)
- 题意翻译:按螺旋方式输出矩阵:先最外圈一圈圈往里。
- 关键思路:用“边界”描述当前还没走过的区域:
- 上边界
top、下边界bottom、左边界left、右边界right。 - 每走完一条边,就把对应边界往里缩一格。
- 上边界
- 为什么要做两次 if 判断?
- 当矩阵变成一行或一列时,走完上边/右边后,可能已经没有下边或左边了;
top<=bottom、left<=right是为了避免重复走/越界。
- 直觉:你可以把它想成“剥洋葱”:每轮剥掉外层四条边,边界往里收缩,直到没有东西可剥。
- 边界判断为什么是两次 if?:当只剩一行或一列时,底边/左边可能不存在,不加判断就会重复输出或越界。
- 复杂度:每个格子输出一次,时间 (O(mn)),空间 (O(1))(不算结果数组)。
类似题目(边界收缩模板)
while (top <= bottom && left <= right) {walkTop(); top++walkRight(); right--if (top <= bottom) { walkBottom(); bottom-- }if (left <= right) { walkLeft(); left++ }}
48. 旋转图像
给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。
你必须在 原地 旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。
示例 1:

输入:matrix = [[1,2,3],[4,5,6],[7,8,9]] 输出:[[7,4,1],[8,5,2],[9,6,3]]
示例 2:

输入:matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]] 输出:[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]
提示:
n == matrix.length == matrix[i].length1 <= n <= 20-1000 <= matrix[i][j] <= 1000
最优解(先转置,再每行翻转)
正在加载编辑器...
最优解讲解(通俗版 + 推理过程)
- 题意翻译:把 (n\times n) 矩阵顺时针旋转 90°,原地完成。
- 关键等价变形:顺时针 90° 的映射是:
- 新位置
(i,j)来自旧位置(n-1-j, i)
- 新位置
- 直接按映射挪会很麻烦:原地替换会覆盖尚未使用的值,需要分圈做四元交换,代码更绕。
- 更好理解的推理:把旋转拆成两步:
- 转置:把行列互换(沿主对角线翻折),
(i,j) -> (j,i) - 每行翻转:把转置后的每一行左右翻转 组合起来恰好等价于顺时针 90°。
- 转置:把行列互换(沿主对角线翻折),
- 为什么这两步刚好等价?:
转置把(n-1-j, i)变成(i, n-1-j)(落到第 i 行),再翻转一行把列n-1-j变成j,于是得到(i,j)。 - 复杂度:两次原地操作(转置 + 翻转),时间 (O(n^2)),额外空间 (O(1))。
类似题目(矩阵变换:用“拆解操作”代替复杂的原地搬运)
// 常见拆解:转置 + 翻转行/列;或按圈做四元交换
240. 搜索二维矩阵 II
编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性:
- 每行的元素从左到右升序排列。
- 每列的元素从上到下升序排列。
示例 1:
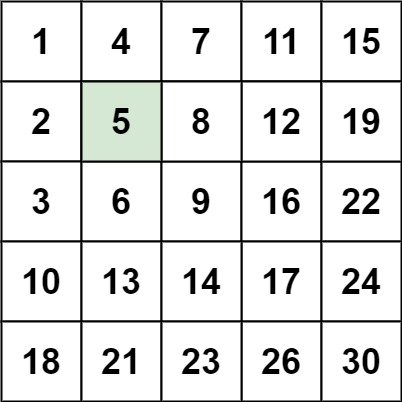
输入:matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5 输出:true
示例 2:
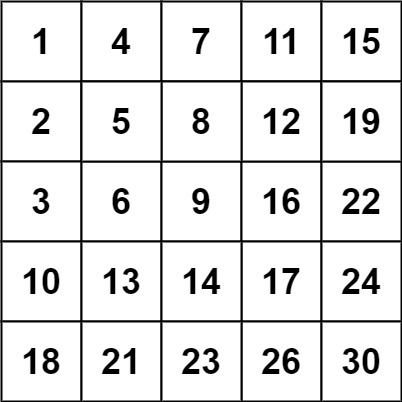
输入:matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20 输出:false
提示:
m == matrix.lengthn == matrix[i].length1 <= n, m <= 300-109 <= matrix[i][j] <= 109- 每行的所有元素从左到右升序排列
- 每列的所有元素从上到下升序排列
-109 <= target <= 109
最优解(从右上角出发:大了左移,小了下移)
正在加载编辑器...
最优解讲解(通俗版 + 推理过程)
- 题目给了两个“单调性”:每行从左到右递增、每列从上到下递增。
- 朴素做法:每行二分或全矩阵扫,能做但还可以更巧妙。
- 关键选择:从右上角开始(也可以从左下角开始):
- 右上角的特点:它的左边都更小,它的下边都更大。
- 推理移动规则:
- 当前值
x:- 如果
x > target:目标更小,只可能在左侧,所以 左移(j--)。 - 如果
x < target:目标更大,只可能在下方,所以 下移(i++)。
- 如果
- 每一步都能排除一整行或一整列的候选区域,所以不会回头。
- 当前值
- 复杂度:最多走
m+n步,时间 (O(m+n)),空间 (O(1))。
类似题目(二维单调矩阵:从角出发“削掉一行/一列”)
let i = 0, j = n - 1while (i < m && j >= 0) {if (a[i][j] === target) return trueif (a[i][j] > target) j--else i++}return false