图论（题单顺序）

本页包含题单「图论」分组的全部题目，顺序与 list.json 保持一致。

200. 岛屿数量

力扣原题：200. 岛屿数量

Medium

深度优先搜索

广度优先搜索

并查集

数组

矩阵

给你一个由 '1'（陆地）和 '0'（水）组成的的二维网格，请你计算网格中岛屿的数量。

岛屿总是被水包围，并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。

此外，你可以假设该网格的四条边均被水包围。

示例 1：

输入：grid = [
  ['1','1','1','1','0'],
  ['1','1','0','1','0'],
  ['1','1','0','0','0'],
  ['0','0','0','0','0']
]
输出：1

示例 2：

输入：grid = [
  ['1','1','0','0','0'],
  ['1','1','0','0','0'],
  ['0','0','1','0','0'],
  ['0','0','0','1','1']
]
输出：3

提示：

m == grid.length
n == grid[i].length
1 <= m, n <= 300
grid[i][j] 的值为 '0' 或 '1'

最优解（DFS/BFS 泛洪：看到 1 就把整座岛“淹掉”并计数）

正在加载编辑器...

Rust 参考（点击展开）

fn num_islands(mut grid: Vec<Vec<u8>>) -> i32 {
    let (m, n) = (grid.len(), grid[0].len());
    fn dfs(grid: &mut Vec<Vec<u8>>, i: usize, j: usize, m: usize, n: usize) {
        if grid[i][j] != b'1' { return; }
        grid[i][j] = b'0';
        if i + 1 < m { dfs(grid, i + 1, j, m, n); }
        if i > 0     { dfs(grid, i - 1, j, m, n); }
        if j + 1 < n { dfs(grid, i, j + 1, m, n); }
        if j > 0     { dfs(grid, i, j - 1, m, n); }
    }
    let mut ans = 0;
    for i in 0..m {
        for j in 0..n {
            if grid[i][j] == b'1' { ans += 1; dfs(&mut grid, i, j, m, n); }
        }
    }
    ans
}

fn g(s: &[&str]) -> Vec<Vec<u8>> { s.iter().map(|r| r.bytes().collect()).collect() }

fn main() {
    println!("{}", num_islands(g(&["11110","11010","11000","00000"]))); // 1
    println!("{}", num_islands(g(&["11000","11000","00100","00011"]))); // 3
    println!("{}", num_islands(g(&["0"]))); // 0
    println!("{}", num_islands(g(&["1"]))); // 1
    println!("{}", num_islands(g(&["101","010","101"]))); // 5
}

最优解讲解（通俗版 + 推理过程）

把岛屿看成“连通块”：上下左右相邻的 '1' 属于同一座岛。
朴素问题：如果你只是计数，不标记，会重复数到同一座岛上的其它格子。
关键推理：每发现一个 '1'，就把整座岛的 '1' 全部标成 '0'：
- 这一步相当于“泛洪填充”（flood fill）。
- 淹完之后，这座岛不会被再次发现，于是计数 +1 是安全的。
为什么是 (O(mn))：每个格子最多被访问一次（从 '1' 变成 '0' 后就不会再次 DFS）。
为什么要“改成 0”而不是只计数？
- 改成 0 本质上就是“做 visited 标记”，让这座岛只会被发现一次，避免重复计数。
边界与实现细节：
- 如果你不想改原网格，也可以用一个 visited 数组记录访问过的格子（空间会变成 (O(mn))）。
复杂度：时间 (O(mn))，递归 DFS 的栈深度最坏 (O(mn))（建议在很大网格时用 BFS 避免爆栈）。

类似题目（网格 DFS/BFS：连通块/泛洪模板）

if cell is target:
  ans++
  floodFill(cell) // 标记 visited

994. 腐烂的橘子

力扣原题：994. 腐烂的橘子

Medium

广度优先搜索

数组

矩阵

在给定的 m x n 网格 grid 中，每个单元格可以有以下三个值之一：

值 0 代表空单元格；
值 1 代表新鲜橘子；
值 2 代表腐烂的橘子。

每分钟，腐烂的橘子 周围 4 个方向上相邻 的新鲜橘子都会腐烂。

返回 直到单元格中没有新鲜橘子为止所必须经过的最小分钟数。如果不可能，返回 -1 。

示例 1：

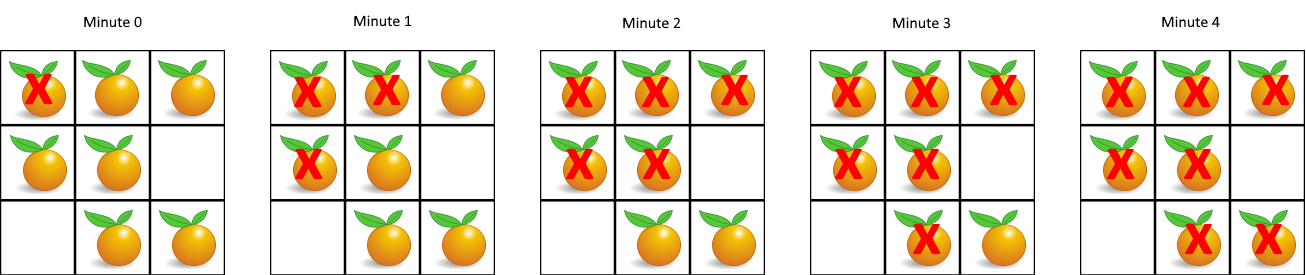
输入：grid = [[2,1,1],[1,1,0],[0,1,1]]
输出：4

示例 2：

输入：grid = [[2,1,1],[0,1,1],[1,0,1]]
输出：-1
解释：左下角的橘子（第 2 行， 第 0 列）永远不会腐烂，因为腐烂只会发生在 4 个方向上。

示例 3：

输入：grid = [[0,2]]
输出：0
解释：因为 0 分钟时已经没有新鲜橘子了，所以答案就是 0 。

提示：

m == grid.length
n == grid[i].length
1 <= m, n <= 10
grid[i][j] 仅为 0、1 或 2

最优解（多源 BFS：所有烂橘子同时扩散）

正在加载编辑器...

Rust 参考（点击展开）

use std::collections::VecDeque;

fn oranges_rotting(mut grid: Vec<Vec<i32>>) -> i32 {
    let (m, n) = (grid.len(), grid[0].len());
    let mut q = VecDeque::new();
    let mut fresh = 0;
    for i in 0..m { for j in 0..n {
        if grid[i][j] == 2 { q.push_back((i, j)); }
        else if grid[i][j] == 1 { fresh += 1; }
    }}
    if fresh == 0 { return 0; }
    let dirs: [(i32,i32); 4] = [(1,0),(-1,0),(0,1),(0,-1)];
    let mut minutes = -1;
    while !q.is_empty() {
        minutes += 1;
        for _ in 0..q.len() {
            let (i, j) = q.pop_front().unwrap();
            for (di, dj) in dirs {
                let ni = i as i32 + di; let nj = j as i32 + dj;
                if ni < 0 || ni >= m as i32 || nj < 0 || nj >= n as i32 { continue; }
                let (ni, nj) = (ni as usize, nj as usize);
                if grid[ni][nj] != 1 { continue; }
                grid[ni][nj] = 2; fresh -= 1; q.push_back((ni, nj));
            }
        }
    }
    if fresh != 0 { -1 } else { minutes }
}

fn main() {
    println!("{}", oranges_rotting(vec![vec![2,1,1],vec![1,1,0],vec![0,1,1]])); // 4
    println!("{}", oranges_rotting(vec![vec![2,1,1],vec![0,1,1],vec![1,0,1]])); // -1
    println!("{}", oranges_rotting(vec![vec![0,2]]));                           // 0
    println!("{}", oranges_rotting(vec![vec![1]]));                             // -1
    println!("{}", oranges_rotting(vec![vec![2,2],vec![1,1],vec![0,1]]));       // 2
}

最优解讲解（通俗版 + 推理过程）

这题的关键是“同时扩散”：每分钟所有烂橘子都会让周围的新鲜橘子变烂。
朴素模拟的坑：如果你一个个烂橘子依次扩散，会把“同一分钟发生的变化”变成先后顺序，时间会被算错。
正确建模：多源 BFS：
- 把所有初始烂橘子都放进队列，作为第 0 层（同一时间的起点）。
- 每一层 BFS 代表 1 分钟扩散：处理当前队列 size 个节点，把能腐烂的新鲜橘子入队。
为什么要维护 fresh 计数？：最后判断是否还有无法被感染的新鲜橘子（被 0 隔离）→ 有则 -1。
为什么 minutes 从 -1 开始？
- BFS 的每一层代表“过了 1 分钟”，但初始腐烂状态并不算过了一分钟，所以先设为 -1；
- 第一次处理初始层后 minutes 变成 0，刚好代表“0 分钟时的状态”。
复杂度：每个格子最多入队一次，时间 (O(mn))，空间 (O(mn))（队列最坏装满网格）。

类似题目（多源 BFS：所有源点同层扩散）

queue = allSources
minutes = -1
while queue:
  minutes++
  process current layer

207. 课程表

力扣原题：207. 课程表

Medium

深度优先搜索

广度优先搜索

图

拓扑排序

你这个学期必须选修 numCourses 门课程，记为 0 到 numCourses - 1 。

在选修某些课程之前需要一些先修课程。先修课程按数组 prerequisites 给出，其中 prerequisites[i] = [a_i, b_i] ，表示如果要学习课程 a_i 则必须先学习课程 b_i。

例如，先修课程对 [0, 1] 表示：想要学习课程 0 ，你需要先完成课程 1 。

请你判断是否可能完成所有课程的学习？如果可以，返回 true ；否则，返回 false 。

示例 1：

输入：numCourses = 2, prerequisites = [[1,0]]
输出：true
解释：总共有 2 门课程。学习课程 1 之前，你需要完成课程 0 。这是可能的。

示例 2：

输入：numCourses = 2, prerequisites = [[1,0],[0,1]]
输出：false
解释：总共有 2 门课程。学习课程 1 之前，你需要先完成课程 0 ；并且学习课程 0 之前，你还应先完成课程 1 。这是不可能的。

提示：

1 <= numCourses <= 2000
0 <= prerequisites.length <= 5000
prerequisites[i].length == 2
0 <= a_i, b_i < numCourses
prerequisites[i] 中的所有课程对 互不相同

最优解（拓扑排序：看是否能处理完所有点）

正在加载编辑器...

Rust 参考（点击展开）

use std::collections::VecDeque;

fn can_finish(num_courses: usize, prerequisites: &[[usize; 2]]) -> bool {
    let mut g = vec![vec![]; num_courses];
    let mut indeg = vec![0usize; num_courses];
    for e in prerequisites {
        let (a, b) = (e[0], e[1]); // b → a
        g[b].push(a);
        indeg[a] += 1;
    }
    let mut q: VecDeque<usize> = (0..num_courses).filter(|&i| indeg[i] == 0).collect();
    let mut taken = 0;
    while let Some(x) = q.pop_front() {
        taken += 1;
        for &y in &g[x] {
            indeg[y] -= 1;
            if indeg[y] == 0 { q.push_back(y); }
        }
    }
    taken == num_courses
}

fn main() {
    println!("{}", can_finish(2, &[[1,0]]));               // true
    println!("{}", can_finish(2, &[[1,0],[0,1]]));         // false
    println!("{}", can_finish(1, &[]));                    // true
    println!("{}", can_finish(3, &[[1,0],[2,1]]));         // true
    println!("{}", can_finish(3, &[[1,0],[2,1],[0,2]]));   // false
}

最优解讲解（通俗版 + 推理过程）

把课程依赖看成有向图：b -> a 表示学 a 之前必须先学 b。
能否学完 ⇔ 图里有没有环：有环就意味着互相依赖，永远无法开始。
拓扑排序的推理：
- 入度为 0 的点表示“没有前置课”，可以立刻学。
- 学完一个课，就相当于把它指向的边删除（后继课程入度减 1）。
- 不断把新的入度为 0 的课加入队列。
- 最后如果学完数量 == 总课程数，说明没有环；否则剩下的点都在环里。
为什么入度为 0 的点一定可以学？：它没有任何前置依赖，放在当前顺序最前面不会违反约束。
为什么处理不完就代表有环？：如果有剩余节点但都入度 > 0，说明它们互相依赖形成闭环，永远不会变成 0 入度。
复杂度：建图 (O(V+E))，拓扑排序 (O(V+E))，空间 (O(V+E))。

类似题目（判断有向图是否有环：Kahn 拓扑）

queue = all nodes with indegree 0
while queue: pop, relax outgoing edges
return processedCount === n

208. 实现 Trie (前缀树)

力扣原题：208. 实现 Trie (前缀树)

Medium

设计

字典树

哈希表

字符串

Trie（发音类似 "try"）或者说 前缀树 是一种树形数据结构，用于高效地存储和检索字符串数据集中的键。这一数据结构有相当多的应用情景，例如自动补全和拼写检查。

请你实现 Trie 类：

Trie() 初始化前缀树对象。
void insert(String word) 向前缀树中插入字符串 word 。
boolean search(String word) 如果字符串 word 在前缀树中，返回 true（即，在检索之前已经插入）；否则，返回 false 。
boolean startsWith(String prefix) 如果之前已经插入的字符串 word 的前缀之一为 prefix ，返回 true ；否则，返回 false 。

示例：

输入
["Trie", "insert", "search", "search", "startsWith", "insert", "search"]
[[], ["apple"], ["apple"], ["app"], ["app"], ["app"], ["app"]]
输出
[null, null, true, false, true, null, true]

解释
Trie trie = new Trie();
trie.insert("apple");
trie.search("apple");   // 返回 True
trie.search("app");     // 返回 False
trie.startsWith("app"); // 返回 True
trie.insert("app");
trie.search("app");     // 返回 True

提示：

1 <= word.length, prefix.length <= 2000
word 和 prefix 仅由小写英文字母组成
insert、search 和 startsWith 调用次数总计不超过 3 * 10⁴ 次

最优解（Trie 节点 = children 映射 + isEnd 标记）

正在加载编辑器...

Rust 参考（点击展开）

use std::collections::HashMap;

#[derive(Default)]
struct Trie {
    children: HashMap<u8, Trie>,
    end: bool,
}

impl Trie {
    fn new() -> Self { Self::default() }
    fn insert(&mut self, word: &str) {
        let mut node = self;
        for b in word.bytes() { node = node.children.entry(b).or_default(); }
        node.end = true;
    }
    fn search(&self, word: &str) -> bool {
        let mut node = self;
        for b in word.bytes() { node = node.children.get(&b)?; }
        node.end
    }
    fn starts_with(&self, prefix: &str) -> bool {
        let mut node = self;
        for b in prefix.bytes() { node = node.children.get(&b)?; }
        true
    }
}

fn main() {
    let mut t = Trie::new();
    t.insert("apple");
    println!("{}", t.search("apple"));     // true
    println!("{}", t.search("app"));       // false
    println!("{}", t.starts_with("app"));  // true
    t.insert("app");
    println!("{}", t.search("app"));       // true
    let mut t2 = Trie::new();
    t2.insert("a");
    println!("{}", t2.search("a"));        // true
    println!("{}", t2.search("ab"));       // false
    println!("{}", t2.starts_with("a"));   // true
}

最优解讲解（通俗版 + 推理过程）

Trie 是干什么的？：专门用来做“字符串前缀查询”的树结构。把单词按字符一层层往下走。
节点需要存什么信息？
- children：从当前节点出发，不同字符的下一步（可以用 Map 或数组 26）。
- end：这个节点是否是某个单词的结尾（解决 “app” 和 “apple” 共用前缀的情况）。
insert 的推理：沿着字符往下走，缺节点就创建，最后把 end 标成 true。
search vs startsWith 的区别：
- search(word) 要求走到最后节点且 end=true。
- startsWith(prefix) 只要路径存在即可，不要求 end。

类似题目（字典树模板）

node = root
for ch in word:
  node = node.children[ch] (create if needed)
node.end = true

图论（题单顺序）

200. 岛屿数量

994. 腐烂的橘子

207. 课程表

208. 实现 Trie (前缀树)

On this page