二叉树（题单顺序）

热题 100 - 二叉树分组（按题单顺序）：94 / 104 / 226 / 101 / 543 / 102 / 108 / 98 / 230 / 199 / 114 / 105 / 437 / 236 / 124

本页包含题单「二叉树」分组的全部题目，顺序与 list.json 保持一致。

说明（点击展开）

为了让测试用例可运行，本页代码里会自带 TreeNode、buildTree 等小工具（不影响 LeetCode 提交）。

94. 二叉树的中序遍历

力扣原题：94. 二叉树的中序遍历

Easy

栈

树

深度优先搜索

二叉树

给定一个二叉树的根节点 root ，返回 它的中序遍历 。

示例 1：

输入：root = [1,null,2,3]
输出：[1,3,2]

示例 2：

输入：root = []
输出：[]

示例 3：

输入：root = [1]
输出：[1]

提示：

树中节点数目在范围 [0, 100] 内
-100 <= Node.val <= 100

进阶: 递归算法很简单，你可以通过迭代算法完成吗？

最优解（迭代栈：一路向左入栈，再回退处理右子树）

正在加载编辑器...

Rust 参考（点击展开）

struct TreeNode { val: i32, left: Option<Box<TreeNode>>, right: Option<Box<TreeNode>> }
fn n(v: i32, l: Option<Box<TreeNode>>, r: Option<Box<TreeNode>>) -> Option<Box<TreeNode>> {
    Some(Box::new(TreeNode { val: v, left: l, right: r }))
}

fn inorder_traversal(root: &Option<Box<TreeNode>>) -> Vec<i32> {
    match root {
        None => vec![],
        Some(node) => {
            let mut res = inorder_traversal(&node.left);
            res.push(node.val);
            res.extend(inorder_traversal(&node.right));
            res
        }
    }
}

fn main() {
    // [1,null,2,3]
    let t1 = n(1, None, n(2, n(3,None,None), None));
    println!("{:?}", inorder_traversal(&t1)); // [1, 3, 2]
    println!("{:?}", inorder_traversal(&None)); // []
    println!("{:?}", inorder_traversal(&n(1,None,None))); // [1]
    println!("{:?}", inorder_traversal(&n(2,n(1,None,None),n(3,None,None)))); // [1, 2, 3]
    let t5 = n(3, n(1,None,n(2,None,None)), n(4,None,None));
    println!("{:?}", inorder_traversal(&t5)); // [1, 2, 3, 4]
}

最优解讲解（通俗版 + 推理过程）

中序遍历顺序：左 → 根 → 右。
递归很好写，但迭代要自己维护“回来的路”：这条“回来的路”就是栈。
推理流程：
- 只要能往左走，就一直把节点压栈（表示“我回来还要处理它和它的右子树”）。
- 走到最左空了，就弹栈：此时左边都处理完了，轮到“根”。
- 处理完根后，再去它的右子树，重复上述过程。
不变量：栈里存的是“左子树已经走到底但根还没输出”的节点路径。
为什么一定按这个顺序压栈/弹栈？
- 你可以把它当成“手动展开递归”：递归在进入左子树前会把当前节点压到调用栈里，等左子树处理完再回来处理根和右子树；迭代栈就是在模拟同一件事。
复杂度：每个节点入栈/出栈各一次，时间 (O(n))；栈深度最多树高 (O(h))。

类似题目（DFS 迭代模板：栈模拟递归）

while (cur || stack.length) {
  while (cur) { stack.push(cur); cur = cur.left }
  cur = stack.pop()
  visit(cur)
  cur = cur.right
}

104. 二叉树的最大深度

力扣原题：104. 二叉树的最大深度

Easy

树

深度优先搜索

广度优先搜索

二叉树

给定一个二叉树 root ，返回其最大深度。

二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。

示例 1：

输入：root = [3,9,20,null,null,15,7]
输出：3

示例 2：

输入：root = [1,null,2]
输出：2

提示：

树中节点的数量在 [0, 10⁴] 区间内。
-100 <= Node.val <= 100

最优解（DFS：深度 = 1 + max(左深, 右深)）

正在加载编辑器...

Rust 参考（点击展开）

struct TreeNode { val: i32, left: Option<Box<TreeNode>>, right: Option<Box<TreeNode>> }
fn n(v: i32, l: Option<Box<TreeNode>>, r: Option<Box<TreeNode>>) -> Option<Box<TreeNode>> {
    Some(Box::new(TreeNode { val: v, left: l, right: r }))
}

fn max_depth(root: &Option<Box<TreeNode>>) -> i32 {
    match root {
        None => 0,
        Some(node) => 1 + max_depth(&node.left).max(max_depth(&node.right)),
    }
}

fn main() {
    let t1 = n(3, n(9,None,None), n(20, n(15,None,None), n(7,None,None)));
    println!("{}", max_depth(&t1));          // 3
    println!("{}", max_depth(&n(1,None,n(2,None,None)))); // 2
    println!("{}", max_depth(&None));        // 0
    println!("{}", max_depth(&n(1,None,None))); // 1
    let t5 = n(1, n(2,n(4,None,None),n(5,None,None)), n(3,None,n(6,None,None)));
    println!("{}", max_depth(&t5));          // 3
}

最优解讲解（通俗版 + 推理过程）

深度的定义：从根到最远叶子的节点数。
关键推理：站在一个节点上，它的最大深度就是：
- 如果是空节点：深度 0
- 否则：1 + max(左子树最大深度, 右子树最大深度)
这就是典型的树形递归：把“大问题”拆成两个子问题。
小例子：根的左子树深度 2、右子树深度 3，那么整棵树深度就是 1 + max(2,3) = 4。
复杂度：每个节点访问一次，时间 (O(n))，递归栈深度 (O(h))。

类似题目（树的高度/深度：1 + max 子树）

if (!node) return 0
return 1 + Math.max(dfs(node.left), dfs(node.right))

226. 翻转二叉树

力扣原题：226. 翻转二叉树

Easy

树

深度优先搜索

广度优先搜索

二叉树

给你一棵二叉树的根节点 root ，翻转这棵二叉树，并返回其根节点。

示例 1：

输入：root = [4,2,7,1,3,6,9]
输出：[4,7,2,9,6,3,1]

示例 2：

输入：root = [2,1,3]
输出：[2,3,1]

示例 3：

输入：root = []
输出：[]

提示：

树中节点数目范围在 [0, 100] 内
-100 <= Node.val <= 100

最优解（递归：交换左右子树）

正在加载编辑器...

Rust 参考（点击展开）

struct TreeNode { val: i32, left: Option<Box<TreeNode>>, right: Option<Box<TreeNode>> }
fn n(v: i32, l: Option<Box<TreeNode>>, r: Option<Box<TreeNode>>) -> Option<Box<TreeNode>> {
    Some(Box::new(TreeNode { val: v, left: l, right: r }))
}

fn invert_tree(root: Option<Box<TreeNode>>) -> Option<Box<TreeNode>> {
    root.map(|mut node| {
        let (l, r) = (node.left.take(), node.right.take());
        node.left = invert_tree(r);
        node.right = invert_tree(l);
        node
    })
}

fn level_order(root: &Option<Box<TreeNode>>) -> Vec<Vec<i32>> {
    use std::collections::VecDeque;
    let Some(r) = root else { return vec![]; };
    let mut q = VecDeque::new();
    q.push_back(r.as_ref());
    let mut res = vec![];
    while !q.is_empty() {
        let size = q.len();
        let mut level = vec![];
        for _ in 0..size {
            let node = q.pop_front().unwrap();
            level.push(node.val);
            if let Some(l) = &node.left { q.push_back(l); }
            if let Some(r) = &node.right { q.push_back(r); }
        }
        res.push(level);
    }
    res
}

fn main() {
    let t1 = n(4, n(2,n(1,None,None),n(3,None,None)), n(7,n(6,None,None),n(9,None,None)));
    println!("{:?}", level_order(&invert_tree(t1))); // [[4], [7, 2], [9, 6, 3, 1]]
    println!("{:?}", level_order(&invert_tree(n(2,n(1,None,None),n(3,None,None))))); // [[2], [3, 1]]
    println!("{:?}", level_order(&invert_tree(None))); // []
}

最优解讲解（通俗版 + 推理过程）

翻转的定义：每个节点都交换它的左子树和右子树。
为什么递归最自然：树的操作通常都是“当前节点做一次操作 + 递归处理子树”。
推理顺序：
- 先把左右子树分别翻转（或者先交换再翻转也行）
- 再把它们互换挂回去
每个节点恰好访问一次，时间 (O(n))。
为什么不会丢节点？：我们只是交换指针指向（left/right），并没有创建/删除节点；递归会把原本的子树继续翻转完再挂回去。
复杂度：时间 (O(n))，递归栈 (O(h))。

类似题目（树结构变换：对每个节点做局部修改）

if (!node) return null
swap(node.left, node.right)
dfs(node.left); dfs(node.right)

101. 对称二叉树

力扣原题：101. 对称二叉树

Easy

树

深度优先搜索

广度优先搜索

二叉树

给你一个二叉树的根节点 root ，检查它是否轴对称。

示例 1：

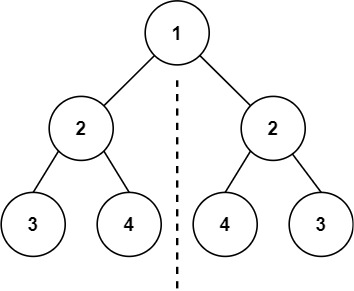
输入：root = [1,2,2,3,4,4,3]
输出：true

示例 2：

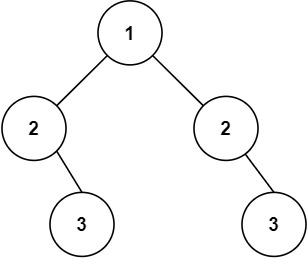
输入：root = [1,2,2,null,3,null,3]
输出：false

提示：

树中节点数目在范围 [1, 1000] 内
-100 <= Node.val <= 100

进阶：你可以运用递归和迭代两种方法解决这个问题吗？

最优解（递归判镜像：左的左 vs 右的右）

正在加载编辑器...

Rust 参考（点击展开）

struct TreeNode { val: i32, left: Option<Box<TreeNode>>, right: Option<Box<TreeNode>> }
fn n(v: i32, l: Option<Box<TreeNode>>, r: Option<Box<TreeNode>>) -> Option<Box<TreeNode>> {
    Some(Box::new(TreeNode { val: v, left: l, right: r }))
}

fn is_mirror(a: &Option<Box<TreeNode>>, b: &Option<Box<TreeNode>>) -> bool {
    match (a, b) {
        (None, None) => true,
        (Some(x), Some(y)) => x.val == y.val
            && is_mirror(&x.left, &y.right)
            && is_mirror(&x.right, &y.left),
        _ => false,
    }
}
fn is_symmetric(root: &Option<Box<TreeNode>>) -> bool {
    is_mirror(root, root)
}

fn main() {
    let t1 = n(1, n(2,n(3,None,None),n(4,None,None)), n(2,n(4,None,None),n(3,None,None)));
    println!("{}", is_symmetric(&t1)); // true
    let t2 = n(1, n(2,None,n(3,None,None)), n(2,None,n(3,None,None)));
    println!("{}", is_symmetric(&t2)); // false
    println!("{}", is_symmetric(&None)); // true
    println!("{}", is_symmetric(&n(1,None,None))); // true
    let t5 = n(1, n(2,n(2,None,None),None), n(2,None,None));
    println!("{}", is_symmetric(&t5)); // false
}

最优解讲解（通俗版 + 推理过程）

对称的本质不是“值相同”这么简单，而是结构和对应位置都要像镜子一样。
关键推理：把问题改成“判断两棵树是否互为镜像”：
- 两棵树镜像 ⇔ 根值相同，且：
  - 左树的左子树 ⇔ 右树的右子树
  - 左树的右子树 ⇔ 右树的左子树
用递归对这两对关系做同样检查即可。
最常见的坑：只比较“每层值是否对称”是不够的，结构（空节点位置）也必须对称。
复杂度：每个节点最多比较一次，时间 (O(n))，递归栈 (O(h))。

类似题目（双树比较：结构 + 值）

if (!a && !b) return true
if (!a || !b) return false
return a.val === b.val && dfs(a.left, b.right) && dfs(a.right, b.left)

543. 二叉树的直径

力扣原题：543. 二叉树的直径

Easy

树

深度优先搜索

二叉树

给你一棵二叉树的根节点，返回该树的直径。

二叉树的直径是指树中任意两个节点之间最长路径的长度。这条路径可能经过也可能不经过根节点 root 。

两节点之间路径的长度由它们之间边数表示。

示例 1：

输入：root = [1,2,3,4,5]
输出：3
解释：3 ，取路径 [4,2,1,3] 或 [5,2,1,3] 的长度。

示例 2：

输入：root = [1,2]
输出：1

提示：

树中节点数目在范围 [1, 10⁴] 内
-100 <= Node.val <= 100

最优解（DFS 计算高度，顺便更新“经过当前节点的最长路径”）

正在加载编辑器...

Rust 参考（点击展开）

struct TreeNode { val: i32, left: Option<Box<TreeNode>>, right: Option<Box<TreeNode>> }
fn n(v: i32, l: Option<Box<TreeNode>>, r: Option<Box<TreeNode>>) -> Option<Box<TreeNode>> {
    Some(Box::new(TreeNode { val: v, left: l, right: r }))
}

fn diameter_of_binary_tree(root: &Option<Box<TreeNode>>) -> i32 {
    fn height(node: &Option<Box<TreeNode>>, best: &mut i32) -> i32 {
        let Some(n) = node else { return 0; };
        let lh = height(&n.left, best);
        let rh = height(&n.right, best);
        *best = (*best).max(lh + rh);
        1 + lh.max(rh)
    }
    let mut best = 0;
    height(root, &mut best);
    best
}

fn main() {
    let t1 = n(1, n(2,n(4,None,None),n(5,None,None)), n(3,None,None));
    println!("{}", diameter_of_binary_tree(&t1)); // 3
    println!("{}", diameter_of_binary_tree(&n(1,n(2,None,None),None))); // 1
    println!("{}", diameter_of_binary_tree(&n(1,None,None)));           // 0
    println!("{}", diameter_of_binary_tree(&None));                      // 0
    let t5 = n(4, n(2,n(1,None,None),n(3,None,None)), n(7,n(6,None,None),n(9,None,None)));
    println!("{}", diameter_of_binary_tree(&t5)); // 4
}

最优解讲解（通俗版 + 推理过程）

直径是什么：任意两点之间最长路径的边数，不一定经过根。
朴素想法：枚举每个节点作为路径拐点再算，容易重复计算。
关键推理：直径一定是某个节点的“左最高 + 右最高”：
- 如果最长路径经过某节点，那么它从左子树某叶子走到右子树某叶子。
- 这条路径长度就是“左子树高度 + 右子树高度”（按边数）。
所以我们写一个求高度的 DFS，同时在每个节点更新一次 best，一趟 DFS 就搞定。
为什么能用“高度”来表达？：经过当前节点的最长路径，一定由“左边最深叶子到当前节点” + “右边最深叶子到当前节点”拼起来，而这两段长度就是左右高度。
复杂度：后序遍历一次，时间 (O(n))，递归栈 (O(h))。

类似题目（后序 DFS：返回高度/贡献，顺便更新全局答案）

function dfs(node){
  lh = dfs(node.left); rh = dfs(node.right)
  best = max(best, combine(lh,rh))
  return 1 + max(lh,rh)
}

102. 二叉树的层序遍历

力扣原题：102. 二叉树的层序遍历

Medium

树

广度优先搜索

二叉树

给你二叉树的根节点 root ，返回其节点值的 层序遍历 。（即逐层地，从左到右访问所有节点）。

示例 1：

输入：root = [3,9,20,null,null,15,7]
输出：[[3],[9,20],[15,7]]

示例 2：

输入：root = [1]
输出：[[1]]

示例 3：

输入：root = []
输出：[]

提示：

树中节点数目在范围 [0, 2000] 内
-1000 <= Node.val <= 1000

最优解（BFS 队列：按层取 size）

正在加载编辑器...

Rust 参考（点击展开）

use std::collections::VecDeque;
struct TreeNode { val: i32, left: Option<Box<TreeNode>>, right: Option<Box<TreeNode>> }
fn n(v: i32, l: Option<Box<TreeNode>>, r: Option<Box<TreeNode>>) -> Option<Box<TreeNode>> {
    Some(Box::new(TreeNode { val: v, left: l, right: r }))
}

fn level_order(root: &Option<Box<TreeNode>>) -> Vec<Vec<i32>> {
    let Some(r) = root else { return vec![]; };
    let mut q = VecDeque::new();
    q.push_back(r.as_ref());
    let mut res = vec![];
    while !q.is_empty() {
        let size = q.len();
        let mut level = vec![];
        for _ in 0..size {
            let node = q.pop_front().unwrap();
            level.push(node.val);
            if let Some(l) = &node.left { q.push_back(l); }
            if let Some(r) = &node.right { q.push_back(r); }
        }
        res.push(level);
    }
    res
}

fn main() {
    let t1 = n(3, n(9,None,None), n(20,n(15,None,None),n(7,None,None)));
    println!("{:?}", level_order(&t1)); // [[3], [9, 20], [15, 7]]
    println!("{:?}", level_order(&n(1,None,None))); // [[1]]
    println!("{:?}", level_order(&None));            // []
    let t4 = n(1, n(2,n(4,None,None),n(5,None,None)), n(3,n(6,None,None),n(7,None,None)));
    println!("{:?}", level_order(&t4)); // [[1], [2, 3], [4, 5, 6, 7]]
}

最优解讲解（通俗版 + 推理过程）

层序遍历就是 BFS：从根开始，一层一层往下扩散。
怎么分层？：在进入一层时，队列里正好存着这一层所有节点，所以先记录 size = q.length，然后弹出 size 次就是这一层。
不变量：每轮循环开始时，队列只包含“当前层”的节点；处理完 size 个后，队列里变成“下一层”的节点。
为什么 size 必须先存下来？：因为你在处理这一层时会不断 push 子节点进队列，如果不锁定 size，就会把下一层也混进当前层。
复杂度：每个节点进队/出队一次，时间 (O(n))，空间 (O(w))（w 为最大层宽）。

类似题目（按层 BFS 模板）

while (q.length) {
  size = q.length
  for i in 1..size: pop + push children
}

108. 将有序数组转换为二叉搜索树

力扣原题：108. 将有序数组转换为二叉搜索树

Easy

树

二叉搜索树

数组

分治

二叉树

给你一个整数数组 nums ，其中元素已经按升序排列，请你将其转换为一棵平衡二叉搜索树。

示例 1：

输入：nums = [-10,-3,0,5,9]
输出：[0,-3,9,-10,null,5]
解释：[0,-10,5,null,-3,null,9] 也将被视为正确答案：

示例 2：

输入：nums = [1,3]
输出：[3,1]
解释：[1,null,3] 和 [3,1] 都是高度平衡二叉搜索树。

提示：

1 <= nums.length <= 10⁴
-10⁴ <= nums[i] <= 10⁴
nums 按 严格递增 顺序排列

最优解（分治：取中点当根，左右递归）

正在加载编辑器...

Rust 参考（点击展开）

struct TreeNode { val: i32, left: Option<Box<TreeNode>>, right: Option<Box<TreeNode>> }

fn sorted_array_to_bst(nums: &[i32]) -> Option<Box<TreeNode>> {
    if nums.is_empty() { return None; }
    let mid = nums.len() / 2;
    Some(Box::new(TreeNode {
        val: nums[mid],
        left: sorted_array_to_bst(&nums[..mid]),
        right: sorted_array_to_bst(&nums[mid + 1..]),
    }))
}

fn inorder(root: &Option<Box<TreeNode>>) -> Vec<i32> {
    match root {
        None => vec![],
        Some(n) => {
            let mut r = inorder(&n.left);
            r.push(n.val);
            r.extend(inorder(&n.right));
            r
        }
    }
}

fn main() {
    println!("{:?}", inorder(&sorted_array_to_bst(&[-10,-3,0,5,9]))); // [-10,-3,0,5,9]
    println!("{:?}", inorder(&sorted_array_to_bst(&[1,3])));           // [1,3]
    println!("{:?}", inorder(&sorted_array_to_bst(&[])));              // []
    println!("{:?}", inorder(&sorted_array_to_bst(&[0])));             // [0]
    println!("{:?}", inorder(&sorted_array_to_bst(&[1,2,3,4,5,6,7]))); // [1,2,3,4,5,6,7]
}

最优解讲解（通俗版 + 推理过程）

要构造“高度平衡”的 BST，直觉就是：根尽量选中间，这样左右子树大小接近。
因为数组有序，取中点做根后：
- 左边部分都比根小 → 递归建左子树
- 右边部分都比根大 → 递归建右子树
递归到区间为空结束。整体时间 (O(n))，每个元素只用一次。
为什么中序遍历能验证结果？：BST 的中序遍历一定是升序；我们用它检查“建出来的树仍能还原原数组”，说明结构符合 BST。
复杂度：时间 (O(n))，递归栈深度 (O(\log n))（平衡时）。

类似题目（分治构造：中点做根/主元）

root = mid
left = build(l, mid-1)
right = build(mid+1, r)

98. 验证二叉搜索树

力扣原题：98. 验证二叉搜索树

Medium

树

深度优先搜索

二叉搜索树

二叉树

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效二叉搜索树定义如下：

节点的左子树只包含 严格小于 当前节点的数。
节点的右子树只包含 严格大于 当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。

示例 1：

输入：root = [2,1,3]
输出：true

示例 2：

输入：root = [5,1,4,null,null,3,6]
输出：false
解释：根节点的值是 5 ，但是右子节点的值是 4 。

提示：

树中节点数目范围在[1, 10⁴] 内
-2³¹ <= Node.val <= 2³¹ - 1

最优解（上下界递归：每个节点都要落在 (min, max) 内）

正在加载编辑器...

Rust 参考（点击展开）

struct TreeNode { val: i32, left: Option<Box<TreeNode>>, right: Option<Box<TreeNode>> }
fn n(v: i32, l: Option<Box<TreeNode>>, r: Option<Box<TreeNode>>) -> Option<Box<TreeNode>> {
    Some(Box::new(TreeNode { val: v, left: l, right: r }))
}

fn is_valid_bst(root: &Option<Box<TreeNode>>) -> bool {
    fn dfs(node: &Option<Box<TreeNode>>, low: i64, high: i64) -> bool {
        let Some(n) = node else { return true; };
        let v = n.val as i64;
        v > low && v < high
            && dfs(&n.left, low, v)
            && dfs(&n.right, v, high)
    }
    dfs(root, i64::MIN, i64::MAX)
}

fn main() {
    println!("{}", is_valid_bst(&n(2,n(1,None,None),n(3,None,None)))); // true
    let t2 = n(5, n(1,None,None), n(4,n(3,None,None),n(6,None,None)));
    println!("{}", is_valid_bst(&t2)); // false
    println!("{}", is_valid_bst(&n(1,n(1,None,None),None))); // false
    println!("{}", is_valid_bst(&None)); // true
    let t5 = n(10, n(5,None,None), n(15,n(6,None,None),n(20,None,None)));
    println!("{}", is_valid_bst(&t5)); // false
}

最优解讲解（通俗版 + 推理过程）

BST 的坑：不是只要 左 < 根 < 右 就行，左子树所有节点都要小于根，右子树所有节点都要大于根。
关键推理：每个节点都有“允许的取值范围”：
- 根：(-∞, +∞)
- 走到左子树：上界变成当前节点值
- 走到右子树：下界变成当前节点值
只要某个节点越界，就不是 BST。
为什么不能只检查父子关系？
- 因为右子树里的某个节点可能比根还小（典型反例：根 5，右子树里出现 3），它和父节点可能仍满足局部大小关系，但整体违反 BST。
复杂度：时间 (O(n))，递归栈 (O(h))。

类似题目（递归传上下界模板）

dfs(node, low, high):
  check low < node.val < high
  dfs(left, low, node.val)
  dfs(right, node.val, high)

230. 二叉搜索树中第 K 小的元素

力扣原题：230. 二叉搜索树中第 K 小的元素

Medium

树

深度优先搜索

二叉搜索树

二叉树

给定一个二叉搜索树的根节点 root ，和一个整数 k ，请你设计一个算法查找其中第 k 小的元素（k 从 1 开始计数）。

示例 1：

输入：root = [3,1,4,null,2], k = 1
输出：1

示例 2：

输入：root = [5,3,6,2,4,null,null,1], k = 3
输出：3

提示：

树中的节点数为 n 。
1 <= k <= n <= 10⁴
0 <= Node.val <= 10⁴

进阶：如果二叉搜索树经常被修改（插入/删除操作）并且你需要频繁地查找第 k 小的值，你将如何优化算法？

最优解（BST 中序遍历就是升序：数到第 k 个）

正在加载编辑器...

Rust 参考（点击展开）

struct TreeNode { val: i32, left: Option<Box<TreeNode>>, right: Option<Box<TreeNode>> }
fn n(v: i32, l: Option<Box<TreeNode>>, r: Option<Box<TreeNode>>) -> Option<Box<TreeNode>> {
    Some(Box::new(TreeNode { val: v, left: l, right: r }))
}

fn kth_smallest(root: &Option<Box<TreeNode>>, k: i32) -> i32 {
    fn inorder(node: &Option<Box<TreeNode>>, k: &mut i32) -> Option<i32> {
        let Some(n) = node else { return None; };
        if let Some(v) = inorder(&n.left, k) { return Some(v); }
        *k -= 1;
        if *k == 0 { return Some(n.val); }
        inorder(&n.right, k)
    }
    inorder(root, &mut k.clone()).unwrap_or(0)
}

fn main() {
    // [3,1,4,null,2], k=1
    let t1 = n(3, n(1,None,n(2,None,None)), n(4,None,None));
    println!("{}", kth_smallest(&t1, 1)); // 1
    println!("{}", kth_smallest(&t1, 2)); // 2
    // [5,3,6,2,4,null,null,1], k=3
    let t3 = n(5, n(3,n(2,n(1,None,None),None),n(4,None,None)), n(6,None,None));
    println!("{}", kth_smallest(&t3, 3)); // 3
    println!("{}", kth_smallest(&n(2,n(1,None,None),n(3,None,None)), 2)); // 2
    println!("{}", kth_smallest(&n(1,None,None), 1)); // 1
}

最优解讲解（通俗版 + 推理过程）

BST 的一个黄金性质：中序遍历（左-根-右）输出的序列一定是从小到大。
所以“第 k 小”就变成：做一次中序遍历，数到第 k 个节点即可。
用迭代栈可以避免递归深度问题；每弹出一次栈，就相当于“访问到一个新的最小值”。
为什么是“弹栈时计数”？
- 因为中序的“访问节点”发生在“左子树处理完之后”，而迭代实现中正对应 cur = stack.pop() 那一刻。
复杂度：最坏要走到第 k 个节点，时间 (O(h+k))（最坏 (O(n))），空间 (O(h))。

类似题目（BST 的顺序统计：中序 + 计数）

inorder: visitCount++; if visitCount==k return node.val

199. 二叉树的右视图

力扣原题：199. 二叉树的右视图

Medium

树

深度优先搜索

广度优先搜索

二叉树

给定一个二叉树的 根节点 root，想象自己站在它的右侧，按照从顶部到底部的顺序，返回从右侧所能看到的节点值。

示例 1：

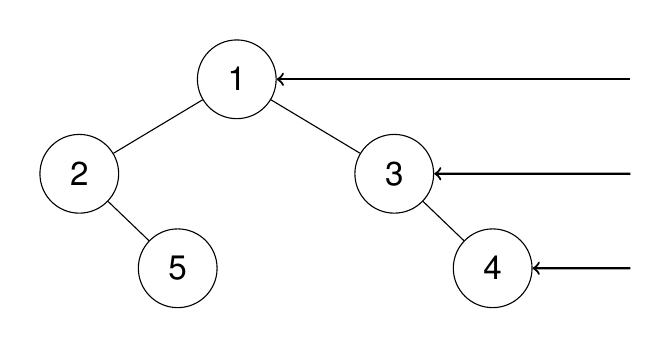
输入：root = [1,2,3,null,5,null,4]

输出：[1,3,4]

解释：

示例 2：

输入：root = [1,2,3,4,null,null,null,5]

输出：[1,3,4,5]

解释：

示例 3：

输入：root = [1,null,3]

输出：[1,3]

示例 4：

输入：root = []

输出：[]

提示:

二叉树的节点个数的范围是 [0,100]
-100 <= Node.val <= 100

最优解（BFS 按层：每层最后一个就是右视图）

正在加载编辑器...

Rust 参考（点击展开）

use std::collections::VecDeque;
struct TreeNode { val: i32, left: Option<Box<TreeNode>>, right: Option<Box<TreeNode>> }
fn n(v: i32, l: Option<Box<TreeNode>>, r: Option<Box<TreeNode>>) -> Option<Box<TreeNode>> {
    Some(Box::new(TreeNode { val: v, left: l, right: r }))
}

fn right_side_view(root: &Option<Box<TreeNode>>) -> Vec<i32> {
    let Some(r) = root else { return vec![]; };
    let mut q = VecDeque::new();
    q.push_back(r.as_ref());
    let mut res = vec![];
    while !q.is_empty() {
        let size = q.len();
        for i in 0..size {
            let node = q.pop_front().unwrap();
            if let Some(l) = &node.left { q.push_back(l); }
            if let Some(r) = &node.right { q.push_back(r); }
            if i == size - 1 { res.push(node.val); }
        }
    }
    res
}

fn main() {
    let t1 = n(1, n(2,None,n(5,None,None)), n(3,None,n(4,None,None)));
    println!("{:?}", right_side_view(&t1)); // [1, 3, 4]
    println!("{:?}", right_side_view(&n(1,None,n(3,None,None)))); // [1, 3]
    println!("{:?}", right_side_view(&None));                       // []
    let t4 = n(1, n(2,n(4,None,None),None), n(3,None,None));
    println!("{:?}", right_side_view(&t4)); // [1, 3, 4]
}

最优解讲解（通俗版 + 推理过程）

右视图的含义：从右侧看过去，每一层你能看到的“最右边”那个节点。
关键推理：按层遍历时，每层的最后一个节点就是最右边：
- BFS 队列一次弹出一层 size 个节点；
- 第 size-1 个弹出的就是这一层的最右节点（与入队顺序无关，只要同层都处理到即可）。
另一种等价做法是 DFS 先走右子树并记录“第一次到达某层”的节点。
为什么“最后一个”一定是可见的？：同层节点从左到右排列，右侧视角只能看到最右端的那个（其它都被挡住）。
复杂度：时间 (O(n))，空间 (O(w))。

类似题目（按层取特征：每层第一个/最后一个）

for each level:
  if i==0 take left view
  if i==size-1 take right view

114. 二叉树展开为链表

力扣原题：114. 二叉树展开为链表

Medium

栈

树

深度优先搜索

链表

二叉树

给你二叉树的根结点 root ，请你将它展开为一个单链表：

展开后的单链表应该同样使用 TreeNode ，其中 right 子指针指向链表中下一个结点，而左子指针始终为 null 。
展开后的单链表应该与二叉树 先序遍历 顺序相同。

示例 1：

输入：root = [1,2,5,3,4,null,6]
输出：[1,null,2,null,3,null,4,null,5,null,6]

示例 2：

输入：root = []
输出：[]

示例 3：

输入：root = [0]
输出：[0]

提示：

树中结点数在范围 [0, 2000] 内
-100 <= Node.val <= 100

进阶：你可以使用原地算法（O(1) 额外空间）展开这棵树吗？

最优解（反向前序：右→左→根，用 prev 串起来）

正在加载编辑器...

Rust 参考（点击展开）

struct TreeNode { val: i32, left: Option<Box<TreeNode>>, right: Option<Box<TreeNode>> }
fn n(v: i32, l: Option<Box<TreeNode>>, r: Option<Box<TreeNode>>) -> Option<Box<TreeNode>> {
    Some(Box::new(TreeNode { val: v, left: l, right: r }))
}

fn flatten(root: Option<Box<TreeNode>>) -> Option<Box<TreeNode>> {
    // 前序遍历收集所有值，再重建右链
    fn preorder(node: &Option<Box<TreeNode>>, vals: &mut Vec<i32>) {
        if let Some(n) = node {
            vals.push(n.val);
            preorder(&n.left, vals);
            preorder(&n.right, vals);
        }
    }
    let mut vals = vec![];
    preorder(&root, &mut vals);
    let mut head = None;
    for &v in vals.iter().rev() {
        head = Some(Box::new(TreeNode { val: v, left: None, right: head }));
    }
    head
}

fn to_right_list(mut root: &Option<Box<TreeNode>>) -> Vec<i32> {
    let mut res = vec![];
    while let Some(n) = root { res.push(n.val); root = &n.right; }
    res
}

fn main() {
    let t1 = n(1, n(2,n(3,None,None),n(4,None,None)), n(5,None,n(6,None,None)));
    println!("{:?}", to_right_list(&flatten(t1))); // [1,2,3,4,5,6]
    println!("{:?}", to_right_list(&flatten(None))); // []
    println!("{:?}", to_right_list(&flatten(n(0,None,None)))); // [0]
    println!("{:?}", to_right_list(&flatten(n(1,None,n(2,n(3,None,None),None))))); // [1,2,3]
    println!("{:?}", to_right_list(&flatten(n(1,n(2,None,None),None)))); // [1,2]
}

最优解讲解（通俗版 + 推理过程）

目标结构：按前序遍历顺序，把树“拉直”成只用 right 指针的链表，且 left 全部置空。
关键推理：如果我们从后往前把节点串起来会更容易：
- 最终链表的“下一个”是谁？就是前序遍历里当前节点的下一个节点。
- 反过来想：如果我们按“前序的逆序”遍历（右→左→根），就能在回溯时用一个 prev 指针把链表串起来：
  - 当前节点的 right 指向 prev
  - 更新 prev = 当前节点
为什么是右→左→根？：前序是根→左→右，逆过来就是右→左→根。
为什么要把 left 置空？：题目要求展开后是“只用 right 指针”的链表，如果 left 不置空就不符合输出结构。
复杂度：每个节点访问一次，时间 (O(n))，递归栈 (O(h))。

类似题目（反向遍历 + prev 指针重建链）

dfs(node.right); dfs(node.left)
node.right = prev; node.left = null; prev = node

105. 从前序与中序遍历序列构造二叉树

力扣原题：105. 从前序与中序遍历序列构造二叉树

Medium

树

数组

哈希表

分治

二叉树

给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

示例 1:

输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]

示例 2:

输入: preorder = [-1], inorder = [-1]
输出: [-1]

提示:

1 <= preorder.length <= 3000
inorder.length == preorder.length
-3000 <= preorder[i], inorder[i] <= 3000
preorder 和 inorder 均 无重复 元素
inorder 均出现在 preorder
preorder 保证为二叉树的前序遍历序列
inorder 保证为二叉树的中序遍历序列

最优解（分治：前序定根，中序切左右）

正在加载编辑器...

Rust 参考（点击展开）

use std::collections::HashMap;
struct TreeNode { val: i32, left: Option<Box<TreeNode>>, right: Option<Box<TreeNode>> }

fn build_tree(preorder: &[i32], inorder: &[i32]) -> Option<Box<TreeNode>> {
    if preorder.is_empty() { return None; }
    let idx: HashMap<i32, usize> = inorder.iter().enumerate().map(|(i,&v)|(v,i)).collect();
    fn helper(pre: &[i32], ino: &[i32], pos: &mut usize, idx: &HashMap<i32,usize>, il: usize, ir: usize) -> Option<Box<TreeNode>> {
        if il > ir || *pos >= pre.len() { return None; }
        let root_val = pre[*pos]; *pos += 1;
        let mid = idx[&root_val];
        Some(Box::new(TreeNode {
            val: root_val,
            left:  helper(pre, ino, pos, idx, il, mid.saturating_sub(1)),
            right: helper(pre, ino, pos, idx, mid + 1, ir),
        }))
    }
    let n = inorder.len();
    helper(preorder, inorder, &mut 0, &idx, 0, n.saturating_sub(1))
}

fn inorder_trav(root: &Option<Box<TreeNode>>) -> Vec<i32> {
    match root {
        None => vec![],
        Some(n) => { let mut r=inorder_trav(&n.left); r.push(n.val); r.extend(inorder_trav(&n.right)); r }
    }
}

fn main() {
    let pre = [3,9,20,15,7]; let ino = [9,3,15,20,7];
    let t = build_tree(&pre, &ino);
    println!("{:?}", inorder_trav(&t)); // [9, 3, 15, 20, 7]
    let pre2 = [1]; let ino2 = [1];
    println!("{:?}", inorder_trav(&build_tree(&pre2, &ino2))); // [1]
    let pre3 = [1,2,3]; let ino3 = [2,1,3];
    println!("{:?}", inorder_trav(&build_tree(&pre3, &ino3))); // [2, 1, 3]
    let pre4 = [1,2]; let ino4 = [2,1];
    println!("{:?}", inorder_trav(&build_tree(&pre4, &ino4))); // [2, 1]
}

最优解讲解（通俗版 + 推理过程）

前序的第一个一定是根：因为前序是根→左→右。
中序里根的位置把左右子树切开：中序是左→根→右，所以根左边都是左子树，根右边都是右子树。
递归构造的推理：
1. 取当前前序指针 prePos 指向的值作为根
2. 在中序中找到根的位置 mid
3. 递归构造左子树（中序区间 [inL, mid-1]）
4. 递归构造右子树（中序区间 [mid+1, inR]）
为什么要 Map 加速？：不然每次找根在中序的位置都要线性搜索，会退化成 (O(n^2))；用 Map 后整体 (O(n))。
为什么递归区间长度正确？
- 中序中 mid 左边的长度就是左子树节点数；而前序会按“根→左→右”消费节点，所以只要用 prePos 作为全局游标，递归自然会按正确数量把节点分配给左/右子树。
复杂度：每个节点只创建一次，查位置 (O(1))，总时间 (O(n))，递归栈 (O(h))。

类似题目（遍历序列建树：一个序列定根，一个序列切左右）

root = preorder[next]
mid = pos[root] in inorder
left = build(inL, mid-1)
right = build(mid+1, inR)

437. 路径总和 III

力扣原题：437. 路径总和 III

Medium

树

深度优先搜索

二叉树

给定一个二叉树的根节点 root ，和一个整数 targetSum ，求该二叉树里节点值之和等于 targetSum 的路径的数目。

路径不需要从根节点开始，也不需要在叶子节点结束，但是路径方向必须是向下的（只能从父节点到子节点）。

示例 1：

输入：root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8
输出：3
解释：和等于 8 的路径有 3 条，如图所示。

示例 2：

输入：root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出：3

提示:

二叉树的节点个数的范围是 [0,1000]
-10⁹ <= Node.val <= 10⁹
-1000 <= targetSum <= 1000

最优解（前缀和 + 哈希：树上也能用“差为 target”）

正在加载编辑器...

Rust 参考（点击展开）

use std::collections::HashMap;
struct TreeNode { val: i32, left: Option<Box<TreeNode>>, right: Option<Box<TreeNode>> }
fn n(v: i32, l: Option<Box<TreeNode>>, r: Option<Box<TreeNode>>) -> Option<Box<TreeNode>> {
    Some(Box::new(TreeNode { val: v, left: l, right: r }))
}

fn path_sum(root: &Option<Box<TreeNode>>, target: i64) -> i32 {
    fn dfs(node: &Option<Box<TreeNode>>, prefix: i64, target: i64, freq: &mut HashMap<i64,i32>, ans: &mut i32) {
        let Some(n) = node else { return; };
        let prefix = prefix + n.val as i64;
        *ans += freq.get(&(prefix - target)).copied().unwrap_or(0);
        *freq.entry(prefix).or_insert(0) += 1;
        dfs(&n.left, prefix, target, freq, ans);
        dfs(&n.right, prefix, target, freq, ans);
        *freq.entry(prefix).or_insert(0) -= 1;
    }
    let mut freq = HashMap::new();
    freq.insert(0, 1);
    let mut ans = 0;
    dfs(root, 0, target, &mut freq, &mut ans);
    ans
}

fn main() {
    // [10,5,-3,3,2,null,11,3,-2,null,1], target=8 → 3
    let t1 = n(10, n(5,n(3,n(3,None,None),n(-2,None,None)),n(2,None,n(1,None,None))), n(-3,None,n(11,None,None)));
    println!("{}", path_sum(&t1, 8)); // 3
    // [5,4,8,11,null,13,4,7,2,null,null,5,1], target=22 → 3
    let t2 = n(5, n(4,n(11,n(7,None,None),n(2,None,None)),None), n(8,n(13,None,None),n(4,n(5,None,None),n(1,None,None))));
    println!("{}", path_sum(&t2, 22)); // 3
    println!("{}", path_sum(&n(1,None,None), 1)); // 1
    println!("{}", path_sum(&None, 0)); // 0
}

最优解讲解（通俗版 + 推理过程）

路径定义：从某个节点往下走到某个节点（必须向下），不要求从根开始，也不要求到叶子结束。
朴素做法：以每个节点为起点做一次 DFS 累加，会重复很多，最坏 (O(n^2))。
关键推理：把树上的“路径和”也写成前缀和差值：
- 在一条从根到当前节点的路径上，设 prefix 是到当前节点的累计和。
- 如果某段向下路径和为 target，就意味着：存在一个祖先前缀 oldPrefix，使得 prefix - oldPrefix = target，也就是 oldPrefix = prefix - target。
- 所以到达一个节点时，只要知道“当前路径上有多少个前缀和等于 prefix-target”，就能一次性统计出所有以当前节点为结尾的合法路径数。
为什么要回溯减频次？
- freq 只应该统计“当前这条根到当前节点路径”上的前缀和。
- DFS 走完一个子树回到父节点时，要把子树路径上的前缀和移除，否则会把另一条分支当成同一路径，统计出错误答案。
为什么这能覆盖“不从根开始”的路径？
- 因为我们统计的是“当前 prefix 与历史 prefix 的差值”，历史 prefix 可以来自任意祖先节点，所以对应的路径起点也可以是任意节点。
复杂度：每个节点进出一次，时间 (O(n))，空间 (O(h))（Map 在一条根到叶路径上的前缀和数量）。

类似题目（树上前缀和模板：进入 +1，离开 -1）

dfs(node, prefix):
  prefix += node.val
  ans += freq[prefix-target]
  freq[prefix]++
  dfs(children)
  freq[prefix]-- // backtrack

236. 二叉树的最近公共祖先

力扣原题：236. 二叉树的最近公共祖先

Medium

树

深度优先搜索

二叉树

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

示例 1：

输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出：3
解释：节点 5 和节点 1 的最近公共祖先是节点 3 。

示例 2：

输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出：5
解释：节点 5 和节点 4 的最近公共祖先是节点 5 。因为根据定义最近公共祖先节点可以为节点本身。

示例 3：

输入：root = [1,2], p = 1, q = 2
输出：1

提示：

树中节点数目在范围 [2, 10⁵] 内。
-10⁹ <= Node.val <= 10⁹
所有 Node.val 互不相同 。
p != q
p 和 q 均存在于给定的二叉树中。

最优解（后序 DFS：左右各返回“是否找到目标”）

正在加载编辑器...

Rust 参考（点击展开）

struct TreeNode { val: i32, left: Option<Box<TreeNode>>, right: Option<Box<TreeNode>> }
fn n(v: i32, l: Option<Box<TreeNode>>, r: Option<Box<TreeNode>>) -> Option<Box<TreeNode>> {
    Some(Box::new(TreeNode { val: v, left: l, right: r }))
}

// 返回 (是否找到, LCA的val或-1)
fn lca(node: &Option<Box<TreeNode>>, p: i32, q: i32) -> (bool, i32) {
    let Some(n) = node else { return (false, -1); };
    let (lf, la) = lca(&n.left, p, q);
    let (rf, ra) = lca(&n.right, p, q);
    if la != -1 { return (true, la); }
    if ra != -1 { return (true, ra); }
    let mid = n.val == p || n.val == q;
    let found = mid || lf || rf;
    let ans = if (mid && (lf || rf)) || (lf && rf) { n.val } else { -1 };
    (found, ans)
}

fn main() {
    // [3,5,1,6,2,0,8,null,null,7,4]
    let t = n(3,
        n(5, n(6,None,None), n(2,n(7,None,None),n(4,None,None))),
        n(1, n(0,None,None), n(8,None,None)));
    println!("{}", lca(&t, 5, 1).1); // 3
    println!("{}", lca(&t, 5, 4).1); // 5
    println!("{}", lca(&n(1,n(2,None,None),None), 1, 2).1); // 1
    println!("{}", lca(&n(1,None,None), 1, 1).1); // 1
    println!("{}", lca(&n(2,n(1,None,None),n(3,None,None)), 1, 3).1); // 2
}

最优解讲解（通俗版 + 推理过程）

最近公共祖先：离 p、q 最近的那个“同时是它们祖先”的节点。
关键推理：后序遍历最合适（先处理子树，再决定当前节点）：
- 让 DFS 返回一个布尔值：当前子树里是否包含 p 或 q。
- 当前节点成为 LCA 的三种情况：
  1. 左子树找到一个，右子树找到一个（分居两侧）
  2. 当前节点本身是 p/q，且左/右子树里找到另一个
一旦满足，就把 ans 记录下来。
为什么要用后序？
- 因为“当前节点是否是 LCA”取决于左右子树各自是否包含目标节点，必须先知道子树结果再做判断（先子后父）。
复杂度：每个节点访问一次，时间 (O(n))，递归栈 (O(h))。

类似题目（后序汇总：子树返回信息，父节点做判断）

left = dfs(left); right = dfs(right); mid = isTarget(node)
if ((left&&right) || (mid&&(left||right))) ans=node
return left || right || mid

124. 二叉树中的最大路径和

力扣原题：124. 二叉树中的最大路径和

Hard

树

深度优先搜索

动态规划

二叉树

二叉树中的路径被定义为一条节点序列，序列中每对相邻节点之间都存在一条边。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点，且不一定经过根节点。

路径和 是路径中各节点值的总和。

给你一个二叉树的根节点 root ，返回其 最大路径和 。

示例 1：

输入：root = [1,2,3]
输出：6
解释：最优路径是 2 -> 1 -> 3 ，路径和为 2 + 1 + 3 = 6

示例 2：

输入：root = [-10,9,20,null,null,15,7]
输出：42
解释：最优路径是 15 -> 20 -> 7 ，路径和为 15 + 20 + 7 = 42

提示：

树中节点数目范围是 [1, 3 * 10⁴]
-1000 <= Node.val <= 1000

最优解（后序 DFS：返回“向上贡献”，同时更新“过当前节点的最优”）

正在加载编辑器...

Rust 参考（点击展开）

struct TreeNode { val: i32, left: Option<Box<TreeNode>>, right: Option<Box<TreeNode>> }
fn n(v: i32, l: Option<Box<TreeNode>>, r: Option<Box<TreeNode>>) -> Option<Box<TreeNode>> {
    Some(Box::new(TreeNode { val: v, left: l, right: r }))
}

fn max_path_sum(root: &Option<Box<TreeNode>>) -> i32 {
    fn dfs(node: &Option<Box<TreeNode>>, best: &mut i32) -> i32 {
        let Some(n) = node else { return 0; };
        let left  = dfs(&n.left,  best).max(0);
        let right = dfs(&n.right, best).max(0);
        *best = (*best).max(n.val + left + right);
        n.val + left.max(right)
    }
    let mut best = i32::MIN;
    dfs(root, &mut best);
    best
}

fn main() {
    println!("{}", max_path_sum(&n(1,n(2,None,None),n(3,None,None)))); // 6
    let t2 = n(-10, n(9,None,None), n(20,n(15,None,None),n(7,None,None)));
    println!("{}", max_path_sum(&t2)); // 42
    println!("{}", max_path_sum(&n(-3,None,None))); // -3
    println!("{}", max_path_sum(&n(2,n(-1,None,None),None))); // 2
    let t5 = n(5, n(4,n(11,n(7,None,None),n(2,None,None)),None), n(8,n(13,None,None),n(4,None,n(1,None,None))));
    println!("{}", max_path_sum(&t5)); // 48
}

最优解讲解（通俗版 + 推理过程）

路径定义：可以从任意节点到任意节点，但必须沿父子连接走；路径可以在某个节点“拐弯”一次（左右各走一段），但不能分叉成三条。
两个概念要分清：
1. 全局最优路径：可能在任意位置拐弯，所以需要一个全局 best。
2. 向上贡献值：返回给父节点时，路径不能左右都拿（否则父节点会分叉），所以只能选“左或右里更大的一边”。
关键推理（后序）：
- 先算出左右子树给你的“向上贡献”；如果贡献是负数，等于拖后腿，直接当 0（不选）。
- 经过当前节点的最佳路径是：node.val + left + right（可以两边都拿，表示在这里拐弯）。
- 但返回给父节点只能是一条：node.val + max(left, right)。
为什么贡献要和 0 比较？
- 因为路径可以从任意节点开始，如果某一侧贡献为负，选上它只会让总和变小，不如直接在当前节点“重新开始”。
复杂度：时间 (O(n))，递归栈 (O(h))。

类似题目（树形 DP：返回局部贡献，更新全局答案）

gain = node.val + max(0, leftGain, rightGain)
best = max(best, node.val + max(0,leftGain) + max(0,rightGain))

二叉树（题单顺序）

On this page