动态规划(题单顺序)
热题 100 - 动态规划分组(按题单顺序):70 / 118 / 198 / 279 / 322 / 139 / 300 / 152 / 416 / 32
本页包含题单「动态规划」分组的全部题目,顺序与 list.json 保持一致。
DP 的核心(点击展开)
把大问题拆成子问题,写出状态含义 + 转移方程 + 初始条件,最后按顺序填表(或滚动变量)。
70. 爬楼梯
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
示例 1:
输入:n = 2 输出:2 解释:有两种方法可以爬到楼顶。 1. 1 阶 + 1 阶 2. 2 阶
示例 2:
输入:n = 3 输出:3 解释:有三种方法可以爬到楼顶。 1. 1 阶 + 1 阶 + 1 阶 2. 1 阶 + 2 阶 3. 2 阶 + 1 阶
提示:
1 <= n <= 45
最优解(DP 滚动:f(n)=f(n-1)+f(n-2))
最优解讲解(通俗版 + 推理过程)
- 先把问题“拆到最后一步”:想到 DP 最常用的入口就是问自己——“到达终点的最后一步从哪来?”
- 到第 n 阶,最后一步只可能是:
- 从
n-1走 1 步上来 - 从
n-2走 2 步上来
- 从
- 到第 n 阶,最后一步只可能是:
- 这一步就是转移方程:设
f(n)为到第 n 阶的方法数,那么:f(n) = f(n-1) + f(n-2)
- 初始条件怎么来的?:
f(1)=1:只有1f(2)=2:1+1或2- 写出来后你会发现它就是斐波那契型 DP。
- 为什么可以用滚动变量?:因为
f(n)只依赖前两项,没必要存整张表。 - 小例子走一遍:
n=4f(1)=1, f(2)=2f(3)=f(2)+f(1)=3f(4)=f(3)+f(2)=5
- 复杂度:时间 (O(n)),空间 (O(1))。
类似题目(线性 DP:只依赖前两项)
for i=3..n: f[i]=f[i-1]+f[i-2]
118. 杨辉三角
给定一个非负整数 numRows,生成「杨辉三角」的前 numRows 行。
在「杨辉三角」中,每个数是它左上方和右上方的数的和。
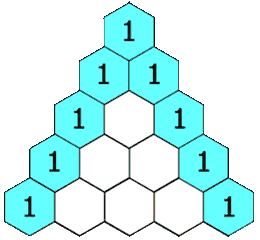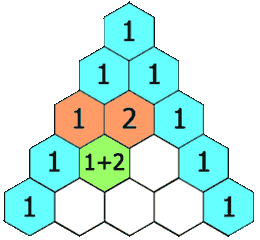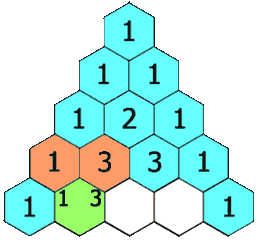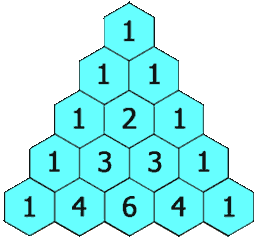
示例 1:
输入: numRows = 5 输出: [[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]
示例 2:
输入: numRows = 1 输出: [[1]]
提示:
1 <= numRows <= 30
最优解(DP:每个格子来自上一行两格之和)
最优解讲解(通俗版 + 推理过程)
- 先观察规律:第 i 行有 i+1 个数,两端永远是 1(因为只能从“边界”一路传下来)。
- 中间格子怎么推出来?:把杨辉三角画出来你会发现,每个中间值正好是上一行的两个“肩膀”之和:
row[j] = prevRow[j-1] + prevRow[j]
- 为什么这是 DP?:
- 状态:
res[i][j](第 i 行第 j 列的值) - 转移:来自上一行的两个相邻状态
- 初始/边界:两端固定为 1
- 状态:
- 小例子走一遍(第 4 行):
- 第 3 行是
[1,2,1] - 第 4 行两端先放 1:
[1,_,_,1] - 中间:
2=1+1、3=2+1→[1,3,3,1]
- 第 3 行是
- 复杂度:生成
numRows行,总元素数约 (O(numRows^2)),时间/空间也是同量级。
类似题目(网格 DP:当前格由上方/左上方转移)
dp[i][j] = dp[i-1][j-1] + dp[i-1][j]
198. 打家劫舍
你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组,计算你 不触动警报装置的情况下 ,一夜之内能够偷窃到的最高金额。
示例 1:
输入:[1,2,3,1] 输出:4 解释:偷窃 1 号房屋 (金额 = 1) ,然后偷窃 3 号房屋 (金额 = 3)。 偷窃到的最高金额 = 1 + 3 = 4 。
示例 2:
输入:[2,7,9,3,1] 输出:12 解释:偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9),接着偷窃 5 号房屋 (金额 = 1)。 偷窃到的最高金额 = 2 + 9 + 1 = 12 。
提示:
1 <= nums.length <= 1000 <= nums[i] <= 400
最优解(DP:抢/不抢当前房子)
最优解讲解(通俗版 + 推理过程)
- 先把约束翻译成人话:相邻房子不能同时抢,所以你在第 i 间房会面临“抢 or 不抢”的二选一。
- 定义状态(这一步决定你是否写得顺):
dp[i]:考虑到前 i 间房(下标 0..i-1)时,能拿到的最大金额。- 也可以用“到下标 i 为止”的写法,本质一样,别混用就行。
- 转移怎么推导出来?只看最后一间房的选择:
- 不抢第 i 间:最大值就是
dp[i-1] - 抢第 i 间:那第 i-1 间不能抢,最大值是
dp[i-2] + nums[i-1] - 所以:
dp[i] = max(dp[i-1], dp[i-2] + nums[i-1]) - 代码里把下标偏移吸收进滚动变量后,就是
max(prev1, prev2 + x)。
- 不抢第 i 间:最大值就是
- 小例子走一遍:
[2,7,9,3,1]- 扫到 2:最好 2
- 扫到 7:
max(2, 0+7)=7 - 扫到 9:
max(7, 2+9)=11 - 扫到 3:
max(11, 7+3)=11 - 扫到 1:
max(11, 11+1)=12
- 为什么能滚动?:每一步只依赖前两步。
- 复杂度:时间 (O(n)),空间 (O(1))。
类似题目(相邻限制 DP)
dp[i] = max(dp[i-1], dp[i-2] + val[i])
279. 完全平方数
给你一个整数 n ,返回 和为 n 的完全平方数的最少数量 。
完全平方数 是一个整数,其值等于另一个整数的平方;换句话说,其值等于一个整数自乘的积。例如,1、4、9 和 16 都是完全平方数,而 3 和 11 不是。
示例 1:
输入:n =12输出:3 解释:12 = 4 + 4 + 4
示例 2:
输入:n =13输出:2 解释:13 = 4 + 9
提示:
1 <= n <= 104
最优解(完全背包 DP:dp[x]=min(dp[x-sq]+1))
最优解讲解(通俗版 + 推理过程)
- 先做一次“问题翻译”:用平方数 (1,4,9,16,\dots) 拼出 n,每个平方数可以重复用,问最少用几个。
- 这就是“硬币无限用、最少个数”的模型 → 完全背包。
- 状态定义:
dp[x]:凑出和为 x 的最少平方数个数(凑不出就当 Infinity)。
- 转移怎么推导:
- 如果最后一个用的是
sq,那前面必须先凑出x - sq,再加上这个sq: - 所以候选是
dp[x - sq] + 1,取所有平方数里的最小值:dp[x] = min(dp[x], dp[x - sq] + 1)
- 如果最后一个用的是
- 为什么内层 x 从小到大?
- 这是“完全背包”的关键:从小到大更新,允许同一个
sq在同一轮里被多次使用。
- 这是“完全背包”的关键:从小到大更新,允许同一个
- 初始化为什么这样设?
dp[0]=0:凑 0 不需要任何数- 其它 Infinity:表示一开始都不可达
- 小例子:
n=12- 平方数:1,4,9
- 最优是
4+4+4→ 3
类似题目(完全背包:最小个数)
dp[0]=0for each coin:for x from coin..n:dp[x]=min(dp[x], dp[x-coin]+1)
322. 零钱兑换
给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。
计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。
你可以认为每种硬币的数量是无限的。
示例 1:
输入:coins =[1, 2, 5], amount =11输出:3解释:11 = 5 + 5 + 1
示例 2:
输入:coins =[2], amount =3输出:-1
示例 3:
输入:coins = [1], amount = 0 输出:0
提示:
1 <= coins.length <= 121 <= coins[i] <= 231 - 10 <= amount <= 104
最优解(完全背包 DP:最少硬币数)
最优解讲解(通俗版 + 推理过程)
- 这题和 279 是同一类:硬币无限用、求最少个数 → 完全背包(最小化)。
- 状态定义:
dp[x]:凑出金额 x 的最少硬币数;凑不出就是 Infinity。
- 转移推导(只看最后一枚硬币):
- 如果最后用的是硬币 c,那么之前必须凑出
x - c,所以候选是dp[x-c] + 1:dp[x] = min(dp[x], dp[x-c] + 1)
- 如果最后用的是硬币 c,那么之前必须凑出
- 为什么外层遍历 coins、内层 x 从 c 到 amount?
- x 从小到大更新,允许“同一枚硬币在同一轮被反复使用”(完全背包特征)。
- 边界与不可达:
dp[0]=0是唯一确定的起点- 若最后
dp[amount]还是 Infinity,说明无论怎么凑都凑不出来 → 返回 -1
- 小例子:
coins=[1,2,5],amount=11- 最优
5+5+1→ 3
- 最优
- 复杂度:时间 (O(amount \cdot #coins)),空间 (O(amount))。
类似题目(完全背包:最少次数/最少步数)
dp[x] = min over choices (dp[x-choice] + cost)
139. 单词拆分
给你一个字符串 s 和一个字符串列表 wordDict 作为字典。如果可以利用字典中出现的一个或多个单词拼接出 s 则返回 true。
注意:不要求字典中出现的单词全部都使用,并且字典中的单词可以重复使用。
示例 1:
输入: s = "leetcode", wordDict = ["leet", "code"] 输出: true 解释: 返回 true 因为 "leetcode" 可以由 "leet" 和 "code" 拼接成。
示例 2:
输入: s = "applepenapple", wordDict = ["apple", "pen"] 输出: true 解释: 返回 true 因为 "applepenapple" 可以由 "apple" "pen" "apple" 拼接成。 注意,你可以重复使用字典中的单词。
示例 3:
输入: s = "catsandog", wordDict = ["cats", "dog", "sand", "and", "cat"] 输出: false
提示:
1 <= s.length <= 3001 <= wordDict.length <= 10001 <= wordDict[i].length <= 20s和wordDict[i]仅由小写英文字母组成wordDict中的所有字符串 互不相同
最优解(DP:dp[i] 表示前 i 个字符能否拆分)
最优解讲解(通俗版 + 推理过程)
- 先把问题改写成“前缀能不能成立”:如果整个字符串能拆分,那么它的某个前缀也一定能拆分。
- 状态定义:
dp[i]:前 i 个字符s[0..i-1]是否能被字典拼出来。dp[0]=true:空串不需要任何单词,也视为可拼(非常关键的起点)。
- 转移推导(枚举最后一个单词):
- 假设最后一个单词是
s[j..i-1],那么必须满足两件事:- 前半段
s[0..j-1]可拼:dp[j] == true - 后半段在字典里:
dict.has(s.slice(j,i))
- 前半段
- 只要存在任意一个 j 满足,就能让
dp[i]=true。
- 假设最后一个单词是
- 为什么是双重循环?:
- 外层 i 逐步扩展前缀长度
- 内层 j 枚举“最后一刀切在哪里”
- 小例子:
leetcode,dict = { "leet", "code" }- 当 i=4 时,j=0,
dp[0]=true且s[0..3]="leet"在 dict →dp[4]=true - 当 i=8 时,j=4,
dp[4]=true且s[4..7]="code"在 dict →dp[8]=true
- 当 i=4 时,j=0,
- 复杂度:最坏 (O(n^2)) 次切片检查(可通过优化字典最大长度等进一步加速),空间 (O(n))。
类似题目(前缀可达性 DP)
dp[0]=truefor i:dp[i]=exists j<i with dp[j] && dict.has(s[j..i])
300. 最长递增子序列
给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。
子序列 是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。
示例 1:
输入:nums = [10,9,2,5,3,7,101,18] 输出:4 解释:最长递增子序列是 [2,3,7,101],因此长度为 4 。
示例 2:
输入:nums = [0,1,0,3,2,3] 输出:4
示例 3:
输入:nums = [7,7,7,7,7,7,7] 输出:1
提示:
1 <= nums.length <= 2500-104 <= nums[i] <= 104
进阶:
- 你能将算法的时间复杂度降低到
O(n log(n))吗?
最优解(贪心 + 二分:耐心排序,O(n log n))
最优解讲解(通俗版 + 推理过程)
- 经典 DP((O(n^2)))能做,但这题最优是 (O(n\log n)),核心在一个很“反直觉”的数组:
tails。 - 状态的“换一种定义”:
tails[len-1]不表示某条具体子序列,而表示:- “长度为 len 的递增子序列,结尾元素能做到的最小值”
- 为什么结尾要尽量小?(关键推理)
- 你可以把“长度相同的子序列”当成同一类竞争者:
- 结尾越小,未来越容易接上一个更大的数继续增长。
- 所以我们宁可保留“更容易扩展”的那条(结尾更小)。
- 你可以把“长度相同的子序列”当成同一类竞争者:
- 更新规则怎么推导:
- 遍历到一个新数 x:
- 如果 x 比所有
tails都大,说明它可以接在最长序列后面 →tails.push(x),长度 +1。 - 否则,它可以“替换”某个长度的结尾,让结尾变得更小、更好扩展:
- 找到第一个
tails[pos] >= x,把tails[pos] = x。
- 找到第一个
- 如果 x 比所有
- 这个 “pos” 用二分找,所以是 (O(\log n))。
- 遍历到一个新数 x:
- 为什么替换不会影响答案长度?
- 替换只是在“同长度”里把结尾压小,不会让已达到的长度变短;
- 反而可能让后续更容易扩展到更长。
- 小例子直觉:
[10,9,2,5,3,7,101,18]- 看到 10 → tails=[10]
- 看到 9 → 替换 tails[0]=9(长度不变,但更好)
- 看到 2 → tails=[2]
- 看到 5 → tails=[2,5]
- 看到 3 → tails=[2,3](把长度 2 的结尾压小)
- … 最终长度是 4
- 复杂度:时间 (O(n\log n)),空间 (O(n))。
类似题目(贪心 + 二分维护“最优结尾”)
pos = lower_bound(tails, x)tails[pos] = x
152. 乘积最大子数组
给你一个整数数组 nums ,请你找出数组中乘积最大的非空连续 子数组(该子数组中至少包含一个数字),并返回该子数组所对应的乘积。
测试用例的答案是一个 32-位 整数。
请注意,一个只包含一个元素的数组的乘积是这个元素的值。
示例 1:
输入: nums = [2,3,-2,4]
输出: 6
解释: 子数组 [2,3] 有最大乘积 6。
示例 2:
输入: nums = [-2,0,-1] 输出: 0 解释: 结果不能为 2, 因为 [-2,-1] 不是子数组。
提示:
1 <= nums.length <= 2 * 104-10 <= nums[i] <= 10nums的任何子数组的乘积都 保证 是一个 32-位 整数
最优解(DP:同时维护 maxProd 与 minProd)
最优解讲解(通俗版 + 推理过程)
- 先对比一下 53(最大和)为什么不够用:
- 求和时,负数只会“拖后腿”,所以一个
cur就能决定“接着累加还是重开”。 - 求乘积时,负数会“翻转正负”,所以“最小乘积”在乘上负数后可能瞬间变成最大。
- 求和时,负数只会“拖后腿”,所以一个
- 状态定义(必须两条线):
maxHere:以当前位置结尾的最大乘积minHere:以当前位置结尾的最小乘积
- 转移推导(只看是否把 x 接上去):
- 以 i 结尾的乘积要么只取
x(重开),要么把 x 接在前一段后面:maxHere = max(x, maxHere*x, minHere*x)minHere = min(x, maxHere*x, minHere*x)
- 以 i 结尾的乘积要么只取
- 代码里用“先在
x < 0时交换 max/min,再更新”来等价实现,更简洁也更不容易写错。 - 为什么
x < 0要 swap?:- 乘以负数后大小关系翻转:原来最大的乘积乘以负数会变成最小,原来最小的乘积乘以负数会变成最大。
- 0 的处理为什么自然正确?
- 当 x=0,
maxHere = max(0, ...)会重开为 0,相当于把子数组切断,符合题意。
- 当 x=0,
- 复杂度:一趟扫描,时间 (O(n)),空间 (O(1))。
类似题目(带符号的 DP:同时维护最大与最小)
if x<0 swap(maxHere, minHere)maxHere = max(x, maxHere*x)minHere = min(x, minHere*x)
416. 分割等和子集
给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。
示例 1:
输入:nums = [1,5,11,5] 输出:true 解释:数组可以分割成 [1, 5, 5] 和 [11] 。
示例 2:
输入:nums = [1,2,3,5] 输出:false 解释:数组不能分割成两个元素和相等的子集。
提示:
1 <= nums.length <= 2001 <= nums[i] <= 100
最优解(0/1 背包:能否凑出 sum/2)
最优解讲解(通俗版 + 推理过程)
- 先做必要的剪枝:如果总和
sum是奇数,无法均分,直接 false。 - 把“分成两堆”改写成“能不能选出一堆和为 target”:
- 只要能选出一个子集和为
target = sum/2,剩下的自然也是target。
- 只要能选出一个子集和为
- 这就是 0/1 背包(可达性版本):
- 每个数只能选 0 次或 1 次(放左边或不放左边)。
- 状态
dp[s]:是否能凑出和 s。 - 初始
dp[0]=true:什么都不选就能凑出 0。
- 转移怎么推导(只看“选不选当前数 x”):
- 不选 x:
dp[s]保持不变 - 选 x:如果之前能凑出
s-x,那现在就能凑出 s - 所以:
dp[s] = dp[s] || dp[s-x]
- 不选 x:
- 为什么 s 要倒序遍历?(最容易踩坑的点)
- 倒序保证每个 x 只被用一次:
- 如果正序更新,
dp[s-x]可能是本轮刚被更新为 true 的,等于把 x 用了多次。
- 如果正序更新,
- 倒序则保证
dp[s-x]还是“上一轮”的状态,符合 0/1 限制。
- 倒序保证每个 x 只被用一次:
- 复杂度:时间 (O(n\cdot target)),空间 (O(target))。
类似题目(0/1 背包可达性:dp 倒序)
for x in nums:for s from target downTo x:dp[s] |= dp[s-x]
32. 最长有效括号
给你一个只包含 '(' 和 ')' 的字符串,找出最长有效(格式正确且连续)括号 子串 的长度。
左右括号匹配,即每个左括号都有对应的右括号将其闭合的字符串是格式正确的,比如 "(()())"。
示例 1:
输入:s = "(()" 输出:2 解释:最长有效括号子串是 "()"
示例 2:
输入:s = ")()())" 输出:4 解释:最长有效括号子串是 "()()"
示例 3:
输入:s = "" 输出:0
提示:
0 <= s.length <= 3 * 104s[i]为'('或')'
最优解(DP:dp[i] 表示以 i 结尾的最长有效长度)
最优解讲解(通俗版 + 推理过程)
- 为什么要用 DP?:这题的难点是“有效串可能嵌套、也可能拼接”,简单用栈能求长度,但 DP 更利于解释“怎么连起来的”。
- 状态定义(必须强调‘以 i 结尾’):
dp[i]:以 i 位置结尾的最长有效括号长度(注意:必须以 i 结尾,不是全局最长)。- 这样做的好处是:我们可以用
dp[i-1]去推dp[i]。
- 只有 ')' 才可能形成有效结尾:
- 如果
s[i]=='(',以它结尾不可能是有效括号串,所以dp[i]=0。
- 如果
- 关键推理:找与 s[i] 匹配的 '(' 在哪里:
- 设
dp[i-1]是 i-1 结尾的有效长度,那么 i 左边最近的一段有效串是:[i-dp[i-1], ..., i-1]
- 如果要让
s[i]这个 ')' 被匹配,它对应的 '(' 必须在这段有效串的前一个位置:j = i - 1 - dp[i-1]
- 设
- 匹配成功时怎么拼长度?(两段合并)
- 若
j>=0且s[j]=='(':- 这对括号贡献
+2 - 中间那段有效串贡献
dp[i-1] - 如果
j-1前面还有一段有效串(形如()(...)的“前缀拼接”),再加dp[j-1]
- 这对括号贡献
- 所以:
dp[i] = dp[i-1] + 2 + (j-1>=0 ? dp[j-1] : 0)
- 若
- 小例子帮助你记住公式:
s="()(())"- 最后一个 ')' 的
dp[i-1]先把"(())"算出来 - 再通过
j找到最左边那对()的拼接位置,把两段连起来
- 最后一个 ')' 的
- 复杂度:时间 (O(n)),空间 (O(n))。
类似题目(dp 记录“以 i 结尾”的最优,靠回看连接)
if s[i]==')':j = i-1-dp[i-1]if s[j]=='(':dp[i]=dp[i-1]+2+dp[j-1]