langShiftlangShift

链表（题单顺序）

热题 100 - 链表分组（按题单顺序）：160 / 206 / 234 / 141 / 142 / 21 / 2 / 19 / 24 / 25 / 138 / 148 / 23 / 146

本页包含题单「链表」分组的全部题目，顺序与 list.json 保持一致。

160. 相交链表

力扣原题：160. 相交链表
Easy
哈希表
链表
双指针

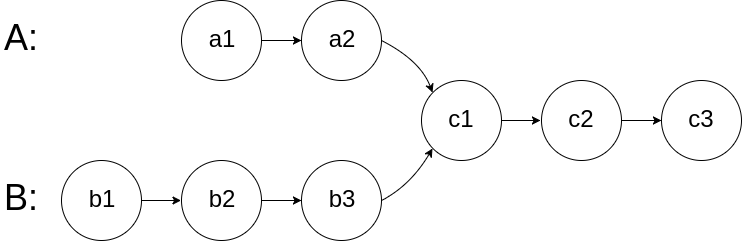
给你两个单链表的头节点 headA 和 headB ，请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点，返回 null 。

图示两个链表在节点 c1 开始相交：

题目数据 保证 整个链式结构中不存在环。

注意，函数返回结果后，链表必须 保持其原始结构 。

自定义评测：

评测系统 的输入如下（你设计的程序 不适用 此输入）：

  • intersectVal - 相交的起始节点的值。如果不存在相交节点，这一值为 0
  • listA - 第一个链表
  • listB - 第二个链表
  • skipA - 在 listA 中（从头节点开始）跳到交叉节点的节点数
  • skipB - 在 listB 中（从头节点开始）跳到交叉节点的节点数

评测系统将根据这些输入创建链式数据结构，并将两个头节点 headA 和 headB 传递给你的程序。如果程序能够正确返回相交节点，那么你的解决方案将被 视作正确答案 。

 

示例 1：

输入：intersectVal = 8, listA = [4,1,8,4,5], listB = [5,6,1,8,4,5], skipA = 2, skipB = 3
输出：Intersected at '8'
解释：相交节点的值为 8 （注意，如果两个链表相交则不能为 0）。
从各自的表头开始算起，链表 A 为 [4,1,8,4,5]，链表 B 为 [5,6,1,8,4,5]。
在 A 中，相交节点前有 2 个节点；在 B 中，相交节点前有 3 个节点。
— 请注意相交节点的值不为 1，因为在链表 A 和链表 B 之中值为 1 的节点 (A 中第二个节点和 B 中第三个节点) 是不同的节点。换句话说，它们在内存中指向两个不同的位置，而链表 A 和链表 B 中值为 8 的节点 (A 中第三个节点，B 中第四个节点) 在内存中指向相同的位置。

 

示例 2：

输入：intersectVal = 2, listA = [1,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1
输出：Intersected at '2'
解释：相交节点的值为 2 （注意，如果两个链表相交则不能为 0）。
从各自的表头开始算起，链表 A 为 [1,9,1,2,4]，链表 B 为 [3,2,4]。
在 A 中，相交节点前有 3 个节点；在 B 中，相交节点前有 1 个节点。

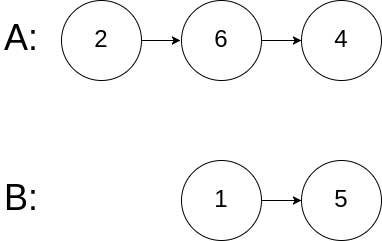
示例 3：

输入：intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2
输出：No intersection
解释：从各自的表头开始算起，链表 A 为 [2,6,4]，链表 B 为 [1,5]。
由于这两个链表不相交，所以 intersectVal 必须为 0，而 skipA 和 skipB 可以是任意值。
这两个链表不相交，因此返回 null 。

 

提示：

  • listA 中节点数目为 m
  • listB 中节点数目为 n
  • 1 <= m, n <= 3 * 104
  • 1 <= Node.val <= 105
  • 0 <= skipA <= m
  • 0 <= skipB <= n
  • 如果 listA 和 listB 没有交点，intersectVal 为 0
  • 如果 listA 和 listB 有交点，intersectVal == listA[skipA] == listB[skipB]

 

进阶：你能否设计一个时间复杂度 O(m + n) 、仅用 O(1) 内存的解决方案？

最优解（双指针走两遍：路程对齐）
正在加载编辑器...
最优解讲解（通俗版 + 推理过程）
  • 题意翻译：两个链表如果相交，后半段会共享同一串节点（内存地址相同，不是值相同）。找第一个共享节点。
  • 朴素思路：用 Set 存 A 的所有节点地址，再扫 B 看第一个命中。能做但要 (O(n)) 额外空间。
  • 想要 (O(1)) 空间，需要“把长度差消掉”。设 A 长 a，B 长 b，相交后共享尾长 c。
  • 关键推理：让两个指针走同样的总路程：
    • 指针 p 先走 A，再走 B；指针 q 先走 B，再走 A。
    • p 走过的总路程是 a + b，q 也是 b + a，所以两者最终会在同一步数上“对齐”。
    • 如果有相交点，它们会在相交点相遇；如果不相交，两者都会在 null 相遇。
  • 直觉类比：两个人从不同起点出发，第一圈走完后交换跑道，再跑一圈，就能把“起点距离终点的差”抵消。
  • 为什么一定不会错过相交点？
    • 假设相交前 A 独有部分长度是 a-c，B 独有部分是 b-c。
    • 当 p 走完 A 的独有部分后进入公共尾巴时，q 可能还在 B 的独有部分；但当两人都各自“换跑道”后，独有部分的长度差会被抵消，最终同时踏入公共尾巴的同一位置。
  • 边界情况：
    • 任一链表为空：直接返回 null（代码里自然成立）。
    • 两条链表本来就是同一个头：第一次比较就相等，直接返回头节点。
  • 复杂度：每个指针最多走 a+b 步，时间 (O(a+b))，空间 (O(1))。
类似题目（双指针对齐路程：先走自己的，再走对方的）
while (p !== q) {

  p = p ? p.next : headB

  q = q ? q.next : headA

}

return p

206. 反转链表

力扣原题：206. 反转链表
Easy
递归
链表
给你单链表的头节点 head ，请你反转链表，并返回反转后的链表。

 

示例 1：

输入：head = [1,2,3,4,5]
输出：[5,4,3,2,1]

示例 2：

输入：head = [1,2]
输出：[2,1]

示例 3：

输入：head = []
输出：[]

 

提示：

  • 链表中节点的数目范围是 [0, 5000]
  • -5000 <= Node.val <= 5000

 

进阶：链表可以选用迭代或递归方式完成反转。你能否用两种方法解决这道题？

最优解（迭代：prev / cur / next 三指针）
正在加载编辑器...
最优解讲解（通俗版 + 推理过程）
  • 链表反转的难点：链表只有 next 指针，一旦你把 cur.next 指向别处，就可能丢失后面的链。
  • 所以必须先“备份后路”：用 nxt = cur.next 先记住下一个节点。
  • 然后做三步循环（这就是反转的本质）：
    1. nxt = cur.next（留后路）
    2. cur.next = prev（把箭头反过来）
    3. prev = cur; cur = nxt（整体往前推进）
  • 不变量：prev 永远是“已经反转好的链表头”，cur 永远指向“还没处理的头”。
  • 为什么必须按这个顺序？
    • 如果你先做 cur.next = prev 再去取 cur.next，你会把原来的后继节点丢掉（因为 cur.next 已经被改写）。
    • 所以“先存后路，再改指针”是链表题最常见的安全写法。
  • 小例子走一遍：1 -> 2 -> 3
    • 初始 prev=null, cur=1
    • 处理 1：nxt=2，1.next=null，prev=1, cur=2
    • 处理 2：nxt=3，2.next=1，prev=2, cur=3
    • 处理 3：nxt=null，3.next=2，结束，prev 就是新头 3。
  • 复杂度：时间 (O(n))，空间 (O(1))。
类似题目（链表指针操作模板）
let prev = null, cur = head

while (cur) {

  const nxt = cur.next

  cur.next = prev

  prev = cur

  cur = nxt

}

return prev

234. 回文链表

力扣原题：234. 回文链表
Easy
栈
递归
链表
双指针

给你一个单链表的头节点 head ，请你判断该链表是否为回文链表。如果是，返回 true ；否则，返回 false 。

 

示例 1：

输入：head = [1,2,2,1]
输出：true

示例 2：

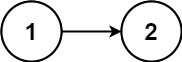
输入：head = [1,2]
输出：false

 

提示：

  • 链表中节点数目在范围[1, 105] 内
  • 0 <= Node.val <= 9

 

进阶：你能否用 O(n) 时间复杂度和 O(1) 空间复杂度解决此题？

最优解（快慢指针找中点 + 反转后半段 + 对比）
正在加载编辑器...
最优解讲解（通俗版 + 推理过程）
  • 朴素思路：把链表转成数组，再用双指针判断回文。简单但需要 (O(n)) 额外空间。
  • 想要更“链表味”的做法：空间 (O(1)) 的关键是：只比较一半，但要让它“方向一致”。
  • 第一步：快慢指针找中点：
    • fast 一次走两步，slow 一次走一步。
    • fast 到尾时，slow 正好到中点附近。
    • 若长度为奇数，中间那个数不影响回文，跳过它即可。
  • 第二步：反转后半段：
    • 回文的定义是“前半段从左到右”要等于“后半段从右到左”。
    • 把后半段反转后，它就变成“从右到左”的顺序摆在链表里，方便直接一对一比较。
  • 第三步：对比两条链：
    • p 从头走，q 从反转后的后半段头走，只要 q 走完仍都相等，就是回文。
  • 为什么只需要比 q 的长度？：后半段长度 ≤ 前半段长度（奇数时前半多一个中点），所以只要后半都匹配就够。
  • 为什么奇数长度要跳过中点？
    • 奇数回文的中间字符没有“镜像对象”，不参与比较；跳过后就能做到左右一一对应。
  • 是否需要把链表再恢复？
    • LeetCode 通常不要求恢复；如果在真实业务里需要保持输入结构，可以在比较后把后半段再反转回去（同样是 (O(n))）。
  • 复杂度：找中点 (O(n)) + 反转 (O(n)) + 比较 (O(n))，总时间 (O(n))，空间 (O(1))。
类似题目（快慢指针 + 反转：对称结构比较）
mid = findMiddle(head)

right = reverse(mid)

return compare(head, right)

141. 环形链表

力扣原题：141. 环形链表
Easy
哈希表
链表
双指针

给你一个链表的头节点 head ，判断链表中是否有环。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。 为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。注意：pos 不作为参数进行传递 。仅仅是为了标识链表的实际情况。

如果链表中存在环 ，则返回 true 。 否则，返回 false 。

 

示例 1：

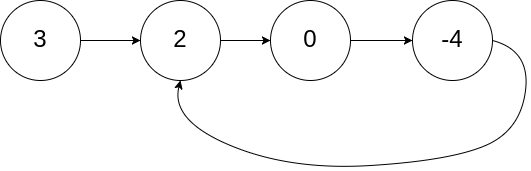
输入：head = [3,2,0,-4], pos = 1
输出：true
解释：链表中有一个环，其尾部连接到第二个节点。

示例 2：

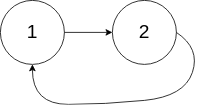
输入：head = [1,2], pos = 0
输出：true
解释：链表中有一个环，其尾部连接到第一个节点。

示例 3：

输入：head = [1], pos = -1
输出：false
解释：链表中没有环。

 

提示：

  • 链表中节点的数目范围是 [0, 104]
  • -105 <= Node.val <= 105
  • pos 为 -1 或者链表中的一个 有效索引 。

 

进阶：你能用 O(1)（即，常量）内存解决此问题吗？

最优解（Floyd 快慢指针：追及相遇）
正在加载编辑器...
最优解讲解（通俗版 + 推理过程）
  • 想法一：用 Set 记录访问过的节点地址，遇到重复就有环。简单但要额外空间。
  • Floyd 的关键直觉：跑步追人：
    • slow 每次走 1 步，fast 每次走 2 步。
    • 如果没环，fast 会先走到 null。
    • 如果有环，fast 会在环里“套圈”追上 slow，一定会相遇（同一条环形跑道，快的人迟早追上慢的人）。
  • 为什么一定相遇？：在环内，fast 相对 slow 每次多走 1 步，相当于在环上每轮把距离缩短 1，距离有限所以必然归零。
  • 为什么没环一定能退出？
    • 因为 fast 走得更快，只要链表是直线，fast 必然先到达 null（或者 fast.next 为 null），循环条件就会失败。
  • 复杂度：时间 (O(n))，空间 (O(1))。
类似题目（快慢指针检测循环/相遇）
while (fast && fast.next) {

  slow = slow.next

  fast = fast.next.next

  if (slow === fast) return true

}

return false

142. 环形链表 II

力扣原题：142. 环形链表 II
Medium
哈希表
链表
双指针

给定一个链表的头节点  head ，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。 为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。

不允许修改 链表。

 

示例 1：

输入：head = [3,2,0,-4], pos = 1
输出：返回索引为 1 的链表节点
解释：链表中有一个环，其尾部连接到第二个节点。

示例 2：

输入：head = [1,2], pos = 0
输出：返回索引为 0 的链表节点
解释：链表中有一个环，其尾部连接到第一个节点。

示例 3：

输入：head = [1], pos = -1
输出：返回 null
解释：链表中没有环。

 

提示：

  • 链表中节点的数目范围在范围 [0, 104] 内
  • -105 <= Node.val <= 105
  • pos 的值为 -1 或者链表中的一个有效索引

 

进阶：你是否可以使用 O(1) 空间解决此题？

最优解（Floyd：相遇后再走一遍找入环点）
正在加载编辑器...
最优解讲解（通俗版 + 推理过程）
  • 第一阶段和 141 一样：用快慢指针判断是否有环，并在环内找到一个相遇点。
  • 第二阶段的“神奇结论”：相遇后，让一个指针从链表头出发，另一个从相遇点出发，都每次走一步，它们会在入环点相遇。
  • 为什么会这样？（核心推理）
    • 设：头到入环点距离为 a，入环点到相遇点距离为 b，环长度为 c。
    • 相遇时：fast 走了 2(a+b)，slow 走了 a+b。
    • 因为 fast 比 slow 多走了一圈或多圈环：2(a+b) - (a+b) = a+b = k*c。
    • 所以 a = k*c - b，也就是：从相遇点再走 a 步，等价于在环上走 k*c - b，最终会回到入环点。
    • 于是：一个从头走 a 步到入环点，另一个从相遇点走 a 步也到入环点 → 相遇即入环点。
  • 小例子直觉：如果入环点在“前面走 a 步”的位置，那么从相遇点再走 a 步，相当于在环上绕若干圈再补齐差距，最终回到同一个入口。
  • 复杂度：第一次相遇 (O(n))，第二次找入口再 (O(n))，总时间 (O(n))，空间 (O(1))。
类似题目（相遇后找入口模板）
meet = getMeetPoint()

if (!meet) return null

let p = head, q = meet

while (p !== q) { p = p.next; q = q.next }

return p

21. 合并两个有序链表

力扣原题：21. 合并两个有序链表
Easy
递归
链表

将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。 

 

示例 1：

输入：l1 = [1,2,4], l2 = [1,3,4]
输出：[1,1,2,3,4,4]

示例 2：

输入：l1 = [], l2 = []
输出：[]

示例 3：

输入：l1 = [], l2 = [0]
输出：[0]

 

提示：

  • 两个链表的节点数目范围是 [0, 50]
  • -100 <= Node.val <= 100
  • l1 和 l2 均按 非递减顺序 排列
最优解（虚拟头结点：像合并两个有序数组）
正在加载编辑器...
最优解讲解（通俗版 + 推理过程）
  • 这题就是“两个有序序列合并”：每次从两个头里挑更小的挂到结果尾部。
  • 虚拟头结点的作用：避免单独处理“结果链表的第一个节点”这种边界；统一用 tail.next = ... 来接。
  • 不变量：dummy.next..tail 永远是已经合并好的有序链表；l1/l2 指向尚未处理的部分。
  • 为什么不会丢节点？
    • 每次只改变 tail.next 指向，并把其中一个链表指针向后移动一步；被接上的节点仍然带着原来的 next，所以链路不断。
  • 稳定性（相等时选谁？）
    • 代码用 <= 先接 l1，这样当值相等时会优先保留 l1 的相对顺序（稳定合并）。
  • 复杂度：每个节点最多访问一次，时间 (O(m+n))，空间 (O(1))（不算输出链表本身）。
类似题目（归并思想：双指针合并）
while (a && b) takeSmaller()

appendRemaining()

2. 两数相加

力扣原题：2. 两数相加
Medium
递归
链表
数学

给你两个 非空 的链表，表示两个非负的整数。它们每位数字都是按照 逆序 的方式存储的，并且每个节点只能存储 一位 数字。

请你将两个数相加，并以相同形式返回一个表示和的链表。

你可以假设除了数字 0 之外，这两个数都不会以 0 开头。

 

示例 1：

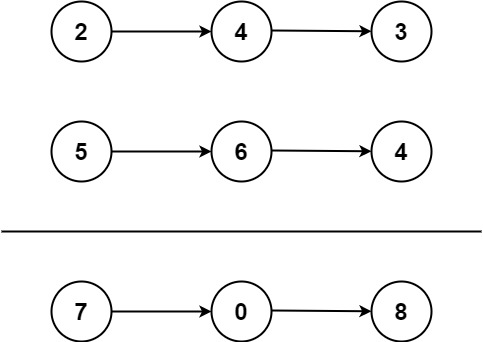
输入：l1 = [2,4,3], l2 = [5,6,4]
输出：[7,0,8]
解释：342 + 465 = 807.

示例 2：

输入：l1 = [0], l2 = [0]
输出：[0]

示例 3：

输入：l1 = [9,9,9,9,9,9,9], l2 = [9,9,9,9]
输出：[8,9,9,9,0,0,0,1]

 

提示：

  • 每个链表中的节点数在范围 [1, 100] 内
  • 0 <= Node.val <= 9
  • 题目数据保证列表表示的数字不含前导零
最优解（逐位相加 + 进位 carry）
正在加载编辑器...
最优解讲解（通俗版 + 推理过程）
  • 题意翻译：两个数用链表的“逆序”存储（个位在头），要求把它们相加并返回同样格式的链表。
  • 逆序的好处：从头开始就是最低位，刚好符合我们做加法的顺序（从个位往高位）。
  • 逐位相加的推理：
    • 每一位都只依赖：这一位的两个数字 + 上一位的进位 carry。
    • sum = a + b + carry，当前位是 sum % 10，新进位是 Math.floor(sum / 10)。
  • 循环条件为什么是 l1 || l2 || carry？：即使两条链都走完了，只要还有进位，也要再生成一个新节点（比如 5+5=10）。
  • 为什么需要 dummy？
    • 和合并链表一样，避免单独处理“结果链表第一个节点”的边界，统一用 tail.next = 新节点。
  • 小例子：342 + 465（链表为 2->4->3 和 5->6->4）
    • 个位：2+5=7（carry 0）
    • 十位：4+6=10 → 写 0，carry=1
    • 百位：3+4+1=8 → 写 8
    • 得到 7->0->8（即 807）
  • 复杂度：时间 (O(m+n))，空间 (O(m+n))（需要新链表）。
类似题目（按位运算：进位 carry 模板）
while (a || b || carry) {

  sum = digit(a) + digit(b) + carry

  carry = Math.floor(sum / base)

  push(sum % base)

}

19. 删除链表的倒数第 N 个结点

力扣原题：19. 删除链表的倒数第 N 个结点
Medium
链表
双指针

给你一个链表，删除链表的倒数第 n 个结点，并且返回链表的头结点。

 

示例 1：

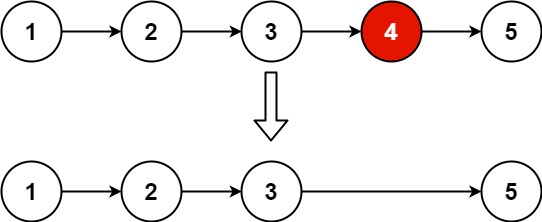
输入：head = [1,2,3,4,5], n = 2
输出：[1,2,3,5]

示例 2：

输入：head = [1], n = 1
输出：[]

示例 3：

输入：head = [1,2], n = 1
输出：[1]

 

提示：

  • 链表中结点的数目为 sz
  • 1 <= sz <= 30
  • 0 <= Node.val <= 100
  • 1 <= n <= sz

 

进阶：你能尝试使用一趟扫描实现吗？

最优解（快慢指针间隔 n：一次遍历定位前驱）
正在加载编辑器...
最优解讲解（通俗版 + 推理过程）
  • 朴素做法：先遍历算长度 len，再走到第 len-n 个节点删除。两趟遍历。
  • 一趟遍历的关键：制造“间隔”：
    • 让 fast 先走 n 步，这样 fast 和 slow 之间就相隔 n 个节点。
    • 当 fast 走到链表末尾时，slow 恰好走到“倒数第 n 个节点的前驱”。
  • 为什么要 dummy？
    • 避免删除头节点时的特殊处理；dummy 永远在 head 前面，删头也等价于普通删除。
  • 为什么 fast 从 dummy 开始更稳？
    • 当要删除的就是头节点（n 等于链表长度）时，slow 仍然能停在 dummy，slow.next 正好是头节点，删除逻辑完全一致。
  • 复杂度：一趟扫描，时间 (O(n))，空间 (O(1))。
类似题目（固定间距双指针模板）
fast 先走 k 步

while (fast) { fast=fast.next; slow=slow.next }

// slow 到达目标位置（或前驱）

24. 两两交换链表中的节点

力扣原题：24. 两两交换链表中的节点
Medium
递归
链表

给你一个链表，两两交换其中相邻的节点，并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题（即，只能进行节点交换）。

 

示例 1：

输入：head = [1,2,3,4]
输出：[2,1,4,3]

示例 2：

输入：head = []
输出：[]

示例 3：

输入：head = [1]
输出：[1]

 

提示：

  • 链表中节点的数目在范围 [0, 100] 内
  • 0 <= Node.val <= 100
最优解（dummy + 指针重连：每次交换一对）
正在加载编辑器...
最优解讲解（通俗版 + 推理过程）
  • 交换的本质不是交换值，是改指针。一对节点 a、b：
    • 原来：prev -> a -> b -> next
    • 目标：prev -> b -> a -> next
  • 按顺序改指针：
    1. a.next = b.next（a 先接到 next，防止断链）
    2. b.next = a（b 指向 a）
    3. prev.next = b（prev 指向新头 b）
  • 为什么 prev 最后要变成 a？：交换后 a 成了这一对的尾巴，下一轮的前驱就是它。
  • 为什么要先做 a.next = b.next？
    • 这是“先保后路”的原则：先让 a 接到后面 next，再把 b 接到 a，最后 prev 接到 b，过程中不会断链。
  • 复杂度：每个节点最多参与一次交换，时间 (O(n))，空间 (O(1))。
类似题目（链表局部重连模板）
// prev -> a -> b -> nxt

a.next = nxt

b.next = a

prev.next = b

prev = a

25. K 个一组翻转链表

力扣原题：25. K 个一组翻转链表
Hard
递归
链表

给你链表的头节点 head ，每 k 个节点一组进行翻转，请你返回修改后的链表。

k 是一个正整数，它的值小于或等于链表的长度。如果节点总数不是 k 的整数倍，那么请将最后剩余的节点保持原有顺序。

你不能只是单纯的改变节点内部的值，而是需要实际进行节点交换。

 

示例 1：

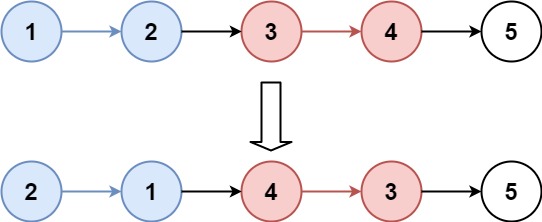
输入：head = [1,2,3,4,5], k = 2
输出：[2,1,4,3,5]

示例 2：

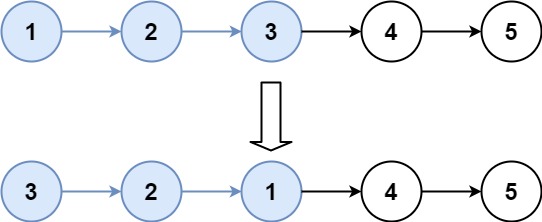
输入：head = [1,2,3,4,5], k = 3
输出：[3,2,1,4,5]

 

提示：
  • 链表中的节点数目为 n
  • 1 <= k <= n <= 5000
  • 0 <= Node.val <= 1000

 

进阶：你可以设计一个只用 O(1) 额外内存空间的算法解决此问题吗？

最优解（分组定位 + 原地翻转 + 接回去）
正在加载编辑器...
最优解讲解（通俗版 + 推理过程）
  • 题意翻译：每 k 个节点为一组翻转，剩下不足 k 个的不动。
  • 为什么不能简单递归反转整个链？：因为要“分组翻转”，组与组之间要正确拼接。
  • 整体策略分三步：
    1. 先确认这一组够不够 k 个：如果不够，直接结束。
    2. 原地反转这一段：反转区间 [start, end] 时，需要知道 end 后面的 groupNext，用于反转时作为初始 prev（这样反转完成后尾巴能自然接回去）。
    3. 把反转后的新头/新尾接回主链：
      • groupPrev.next = newHead
      • 下一组的 groupPrev 更新为 newTail
  • 关键不变量：每完成一组，groupPrev 永远停在“已处理部分的最后一个节点”，下一组从它后面开始。
  • 为什么反转时 prev 初始设为 groupNext？
    • 这样反转完成后，原来的组头（反转后的尾）会自然指向 groupNext，组与组的连接自动正确。
  • 边界情况：
    • k=1：不需要反转，逻辑仍然成立。
    • 剩余不足 k 个：getKth 返回 null，直接停止，尾部保持原样。
  • 复杂度：每个节点最多被反转一次，时间 (O(n))，空间 (O(1))（递归栈为 0，因为是迭代）。
类似题目（区间反转：先找边界，再反转，再接回）
end = getKth(prev, k)

next = end.next

reverse(prev.next .. end) and connect to next

prev = oldHead // 反转后的尾

138. 随机链表的复制

力扣原题：138. 随机链表的复制
Medium
哈希表
链表

给你一个长度为 n 的链表，每个节点包含一个额外增加的随机指针 random ，该指针可以指向链表中的任何节点或空节点。

构造这个链表的 深拷贝。 深拷贝应该正好由 n 个 全新 节点组成，其中每个新节点的值都设为其对应的原节点的值。新节点的 next 指针和 random 指针也都应指向复制链表中的新节点，并使原链表和复制链表中的这些指针能够表示相同的链表状态。复制链表中的指针都不应指向原链表中的节点 。

例如，如果原链表中有 X 和 Y 两个节点，其中 X.random --> Y 。那么在复制链表中对应的两个节点 x 和 y ，同样有 x.random --> y 。

返回复制链表的头节点。

用一个由 n 个节点组成的链表来表示输入/输出中的链表。每个节点用一个 [val, random_index] 表示：

  • val：一个表示 Node.val 的整数。
  • random_index：随机指针指向的节点索引（范围从 0 到 n-1）；如果不指向任何节点，则为  null 。

你的代码 只 接受原链表的头节点 head 作为传入参数。

 

示例 1：

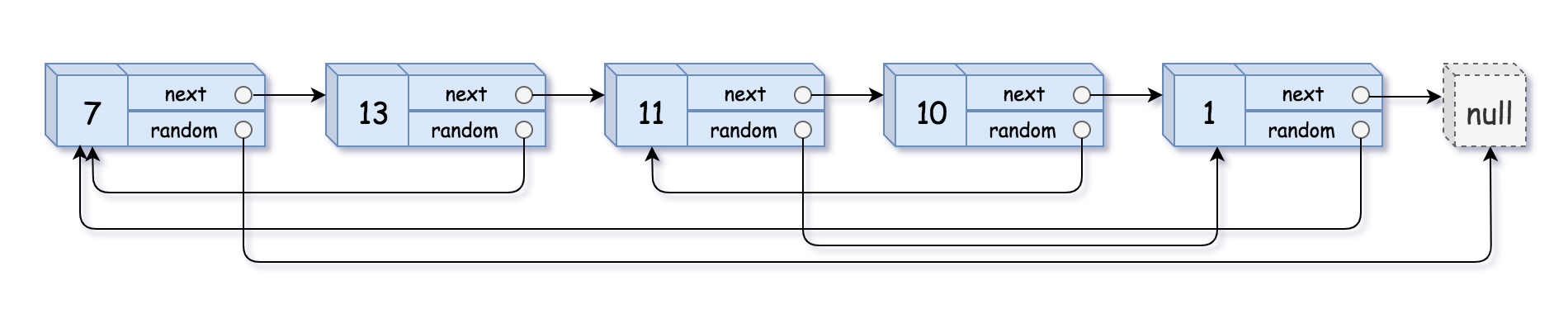
输入：head = [[7,null],[13,0],[11,4],[10,2],[1,0]]
输出：[[7,null],[13,0],[11,4],[10,2],[1,0]]

示例 2：

输入：head = [[1,1],[2,1]]
输出：[[1,1],[2,1]]

示例 3：

输入：head = [[3,null],[3,0],[3,null]]
输出：[[3,null],[3,0],[3,null]]

 

提示：

  • 0 <= n <= 1000
  • -104 <= Node.val <= 104
  • Node.random 为 null 或指向链表中的节点。

 

最优解（哈希表：旧节点 -> 新节点）
正在加载编辑器...
最优解讲解（通俗版 + 推理过程）
  • 难点：random 指针可以指向任意节点甚至自己；直接复制时，你会遇到“指向的目标还没创建”的问题。
  • 关键推理：先把“节点对应关系”建立起来：
    • 第一次遍历：只创建每个新节点，并用 Map<oldNode, newNode> 记住映射。
    • 这一步完成后，所有新节点都已经存在了，后续再补指针就不会缺引用。
  • 第二次遍历：补齐 next/random：
    • new.next = old.next ? map.get(old.next) : null
    • new.random = old.random ? map.get(old.random) : null
  • 为什么要两遍？：一遍做不到“既创建节点又保证 random 目标已存在”；两遍则天然解决“前向引用/后向引用/自引用”。
  • 为什么 Map 的 key 必须是“旧节点对象”而不是值？
    • 因为链表节点值可能重复，能唯一标识节点的是它的“地址/对象引用”，所以必须用旧节点对象作为 key。
  • 复杂度：两趟遍历，时间 (O(n))，空间 (O(n))（Map 保存映射）。
类似题目（图/链表复制：先建点，再连边）
// 1) create all nodes and store mapping

// 2) traverse again to wire pointers/edges using mapping

148. 排序链表

力扣原题：148. 排序链表
Medium
链表
双指针
分治
排序
归并排序

给你链表的头结点 head ，请将其按 升序 排列并返回 排序后的链表 。

 

示例 1：

输入：head = [4,2,1,3]
输出：[1,2,3,4]

示例 2：

输入：head = [-1,5,3,4,0]
输出：[-1,0,3,4,5]

示例 3：

输入：head = []
输出：[]

 

提示：

  • 链表中节点的数目在范围 [0, 5 * 104] 内
  • -105 <= Node.val <= 105

 

进阶：你可以在 O(n log n) 时间复杂度和常数级空间复杂度下，对链表进行排序吗？

最优解（归并排序：分治 + 合并两个有序链表）
正在加载编辑器...
最优解讲解（通俗版 + 推理过程）
  • 链表排序为什么常用归并？：链表不支持随机访问（不能像数组那样快排/堆排方便地按下标交换），但“拆成两半 + 合并”非常适合链表。
  • 归并排序的三步：
    1. 分：用快慢指针找中点，把链表一分为二（并断开连接）。
    2. 治：递归把左右两半分别排好序。
    3. 合：用“合并两个有序链表”把两半合成一个有序链。
  • 为什么时间是 (O(n\log n))：每一层合并总共处理 n 个节点，层数约 (\log n)。
  • 为什么要在中点处“断开”？
    • 如果不把 prev.next = null 断开，左右两半仍然连在一起，递归会陷入死循环或者反复处理同一段链。
  • 空间复杂度提醒：
    • 归并排序的合并是原地重连指针，不需要额外数组；
    • 但递归调用会占用栈深度 (O(\log n))。
类似题目（链表归并排序模板）
mid = splitByFastSlow(head)

left = sort(leftHalf)

right = sort(rightHalf)

return merge(left, right)

23. 合并 K 个升序链表

力扣原题：23. 合并 K 个升序链表
Hard
链表
分治
堆（优先队列）
归并排序

给你一个链表数组，每个链表都已经按升序排列。

请你将所有链表合并到一个升序链表中，返回合并后的链表。

 

示例 1：

输入：lists = [[1,4,5],[1,3,4],[2,6]]
输出：[1,1,2,3,4,4,5,6]
解释：链表数组如下：
[
  1->4->5,
  1->3->4,
  2->6
]
将它们合并到一个有序链表中得到。
1->1->2->3->4->4->5->6

示例 2：

输入：lists = []
输出：[]

示例 3：

输入：lists = [[]]
输出：[]

 

提示：

  • k == lists.length
  • 0 <= k <= 10^4
  • 0 <= lists[i].length <= 500
  • -10^4 <= lists[i][j] <= 10^4
  • lists[i] 按 升序 排列
  • lists[i].length 的总和不超过 10^4
最优解（小根堆：每次取当前最小头结点）
正在加载编辑器...
最优解讲解（通俗版 + 推理过程）
  • 朴素做法：把所有节点都收集到数组里排序再重建，能做但会占用额外空间且丢失“链表合并”的结构优势。
  • 更直接的思路：每次都从 k 个链表的当前头里选最小的那个：
    • 如果你每次线性扫 k 个头去找最小，单步 (O(k))，总节点数为 (N)，总体 (O(Nk))。
  • 关键优化：用小根堆把“找最小”变成 (O(\log k))：
    • 堆里始终放每条链表的当前头结点。
    • 弹出堆顶（最小头），把它接到答案尾部。
    • 然后把它的 next 再放回堆（相当于这条链表推进了一步）。
  • 为什么复杂度是 (O(N\log k))：每个节点都会被 push+pop 一次，堆大小最多 k。
  • 为什么堆里存“节点”而不是“值”？
    • 因为我们需要把弹出的节点直接接到结果链表尾部，同时还要能拿到它的 next 继续推进对应链表。
  • 复杂度总结：时间 (O(N\log k))，空间 (O(k))（堆大小）。
类似题目（多路归并：堆维护“当前最小候选”）
init heap with k heads

while heap not empty:

  x = popMin()

  append x

  if x.next: push(x.next)

146. LRU 缓存

力扣原题：146. LRU 缓存
Medium
设计
哈希表
链表
双向链表
请你设计并实现一个满足  LRU (最近最少使用) 缓存 约束的数据结构。
实现 LRUCache 类：
  • LRUCache(int capacity) 以 正整数 作为容量 capacity 初始化 LRU 缓存
  • int get(int key) 如果关键字 key 存在于缓存中，则返回关键字的值，否则返回 -1 。
  • void put(int key, int value) 如果关键字 key 已经存在，则变更其数据值 value ；如果不存在，则向缓存中插入该组 key-value 。如果插入操作导致关键字数量超过 capacity ，则应该 逐出 最久未使用的关键字。

函数 get 和 put 必须以 O(1) 的平均时间复杂度运行。

 

示例：

输入
["LRUCache", "put", "put", "get", "put", "get", "put", "get", "get", "get"]
[[2], [1, 1], [2, 2], [1], [3, 3], [2], [4, 4], [1], [3], [4]]
输出
[null, null, null, 1, null, -1, null, -1, 3, 4]

解释
LRUCache lRUCache = new LRUCache(2);
lRUCache.put(1, 1); // 缓存是 {1=1}
lRUCache.put(2, 2); // 缓存是 {1=1, 2=2}
lRUCache.get(1);    // 返回 1
lRUCache.put(3, 3); // 该操作会使得关键字 2 作废，缓存是 {1=1, 3=3}
lRUCache.get(2);    // 返回 -1 (未找到)
lRUCache.put(4, 4); // 该操作会使得关键字 1 作废，缓存是 {4=4, 3=3}
lRUCache.get(1);    // 返回 -1 (未找到)
lRUCache.get(3);    // 返回 3
lRUCache.get(4);    // 返回 4

 

提示：

  • 1 <= capacity <= 3000
  • 0 <= key <= 10000
  • 0 <= value <= 105
  • 最多调用 2 * 105 次 get 和 put
最优解（Map + 双向链表：O(1) get/put）
正在加载编辑器...
最优解讲解（通俗版 + 推理过程）
  • LRU 需要支持两件事都很快：
    1. 按 key 快速找到 value（get/put 查找要快）→ 哈希表
    2. 快速把“最近使用”移动到最前、把“最久未使用”从末尾删除 → 双向链表
  • 为什么单用 Map 不够？：JS 的 Map 虽然有插入顺序，但题目语义是“访问会更新顺序”。要做到所有操作明确 (O(1))，最稳的是 Map + 双向链表。
  • 双向链表存什么？：按“最近使用”从前到后排队：
    • 头部附近：最近使用
    • 尾部附近：最久未使用（需要淘汰）
  • 每个操作如何推理到指针动作：
    • get(key)：如果存在，说明被访问了 → 从原位置摘下来，插到链表头部。
    • put(key,val)：
      • key 已存在：更新值，并把它移动到头部（也算“最近使用”）。
      • key 不存在：新建节点插到头部；如果容量超了，删除尾部前一个节点（LRU）。
  • 为什么双向链表必须有 dummy head/tail：避免处理空链/头尾边界，所有插入删除都变成统一的四条指针修改。
  • 核心不变量（保证你不会写崩）
    • 链表顺序永远表示“从最近到最久”：head.next 是最近使用，tail.prev 是最久未使用。
    • map 里的每个 key 都能定位到链表中的一个节点，且节点也能反查自己的 key（用于淘汰时删除 map）。
  • 为什么必须是双向链表而不是单向？
    • 淘汰的是尾部节点；如果只有单向链表，删除尾部需要找到前驱，会退化成 (O(n))。
    • 双向链表能在 (O(1)) 摘除任意节点。
  • 复杂度：get/put 都是均摊 (O(1)) 时间，空间 (O(capacity))。
类似题目（缓存/淘汰策略：Map + 双向链表）
// Map 用来 O(1) 定位节点

// Doubly Linked List 用来 O(1) 调整使用顺序与淘汰尾部

矩阵（题单顺序）

热题 100 - 矩阵分组（按题单顺序）：73 / 54 / 48 / 240

二叉树（题单顺序）

热题 100 - 二叉树分组（按题单顺序）：94 / 104 / 226 / 101 / 543 / 102 / 108 / 98 / 230 / 199 / 114 / 105 / 437 / 236 / 124